DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.43228#0004
4
Kuno Fladt:
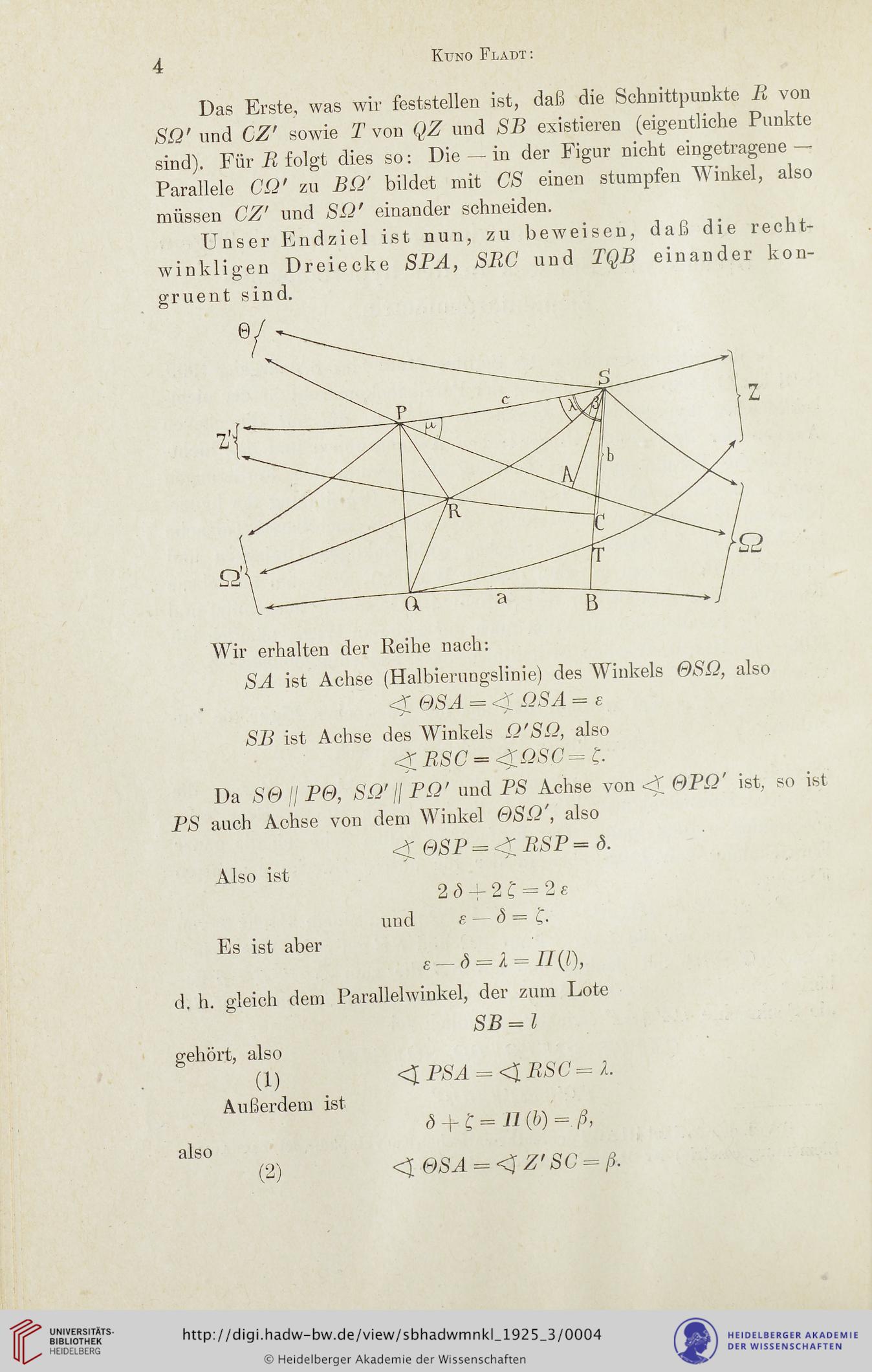
Das Erste, was wir feststellen ist, daß die Schnittpunkte R von
SQ' und GZ' sowie T von QZ und SB existieren (eigentliche Punkte
sind). Für R folgt dies so: Die — in der Figur nicht eingetragene —
Parallele CU' zu BQ' bildet mit CS einen stumpfen Winkel, also
müssen CZ' und SQ' einander schneiden.
Unser Endziel ist nun, zu beweisen, daß die recht-
winkligen Dreiecke SPA, SRC und TQB einander kon-
gruent sind.
Wir erhalten der Reihe nach:
SA ist Achse (Halbierungslinie) des Winkels ©SQ, also
< ©SA = < QSA = e
SB ist Achse des Winkels Q'SQ, also
^RSC = ^QSC=^.
Da S© II P&, SQ' II PQ' und PS Achse von ©PQ' ist, so ist
PS auch Achse von dem Winkel ©SQ', also
< &SP = ^RSP = ö.
Also ist
2 d + 2 C = 2 £
und £ — d = ’Q.
Es ist aber
£ —d = 2 = 7Z(Z),
d. h. gleich dem Parallelwinkel, der zum Lote
SB=l
gehört, also
(1) <^PSA = <$RSC=k
Außerdem ist
d + C = n (d) = ß,
also
(2) <$ &SA = Z'SC = ß.
Kuno Fladt:
Das Erste, was wir feststellen ist, daß die Schnittpunkte R von
SQ' und GZ' sowie T von QZ und SB existieren (eigentliche Punkte
sind). Für R folgt dies so: Die — in der Figur nicht eingetragene —
Parallele CU' zu BQ' bildet mit CS einen stumpfen Winkel, also
müssen CZ' und SQ' einander schneiden.
Unser Endziel ist nun, zu beweisen, daß die recht-
winkligen Dreiecke SPA, SRC und TQB einander kon-
gruent sind.
Wir erhalten der Reihe nach:
SA ist Achse (Halbierungslinie) des Winkels ©SQ, also
< ©SA = < QSA = e
SB ist Achse des Winkels Q'SQ, also
^RSC = ^QSC=^.
Da S© II P&, SQ' II PQ' und PS Achse von ©PQ' ist, so ist
PS auch Achse von dem Winkel ©SQ', also
< &SP = ^RSP = ö.
Also ist
2 d + 2 C = 2 £
und £ — d = ’Q.
Es ist aber
£ —d = 2 = 7Z(Z),
d. h. gleich dem Parallelwinkel, der zum Lote
SB=l
gehört, also
(1) <^PSA = <$RSC=k
Außerdem ist
d + C = n (d) = ß,
also
(2) <$ &SA = Z'SC = ß.