8
Ernst Roeser:
§ 2.
Sphärische Körper.
Um die entsprechenden Körper der nichteuklidischen Geometrie
positiver Krümmung zu erhalten, wenden wir auf die Seiten die für
den reellen Übergang charakteristische Gleichung:
an, d. h. wir ersetzen die Seiten durch die komplementären Parallel-
winkel, die Winkel des rechtwinkligen Dreiecks durch ihre Komplemente.
Hinzu tritt als Neues noch das Vertauschungsgesetz. Diametral gegen-
überliegende Seiten werden vertauscht. Entsprechendes ergibt sich auch
für die Körper. Diese Verhältnisse sind für die Ebene schon erörtert
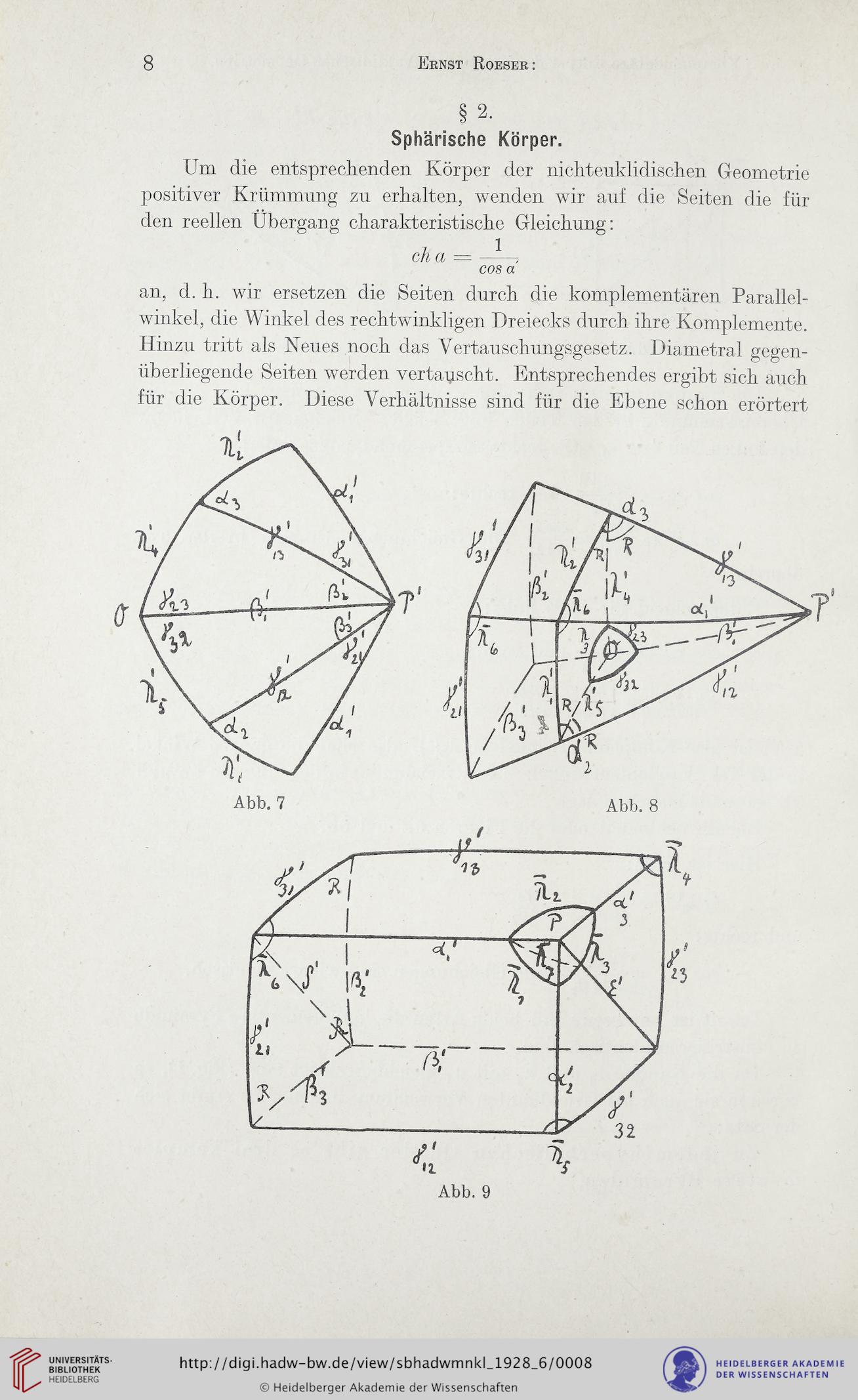
Abb. 7 Abb. 8
Abb. 9
Ernst Roeser:
§ 2.
Sphärische Körper.
Um die entsprechenden Körper der nichteuklidischen Geometrie
positiver Krümmung zu erhalten, wenden wir auf die Seiten die für
den reellen Übergang charakteristische Gleichung:
an, d. h. wir ersetzen die Seiten durch die komplementären Parallel-
winkel, die Winkel des rechtwinkligen Dreiecks durch ihre Komplemente.
Hinzu tritt als Neues noch das Vertauschungsgesetz. Diametral gegen-
überliegende Seiten werden vertauscht. Entsprechendes ergibt sich auch
für die Körper. Diese Verhältnisse sind für die Ebene schon erörtert
Abb. 7 Abb. 8
Abb. 9