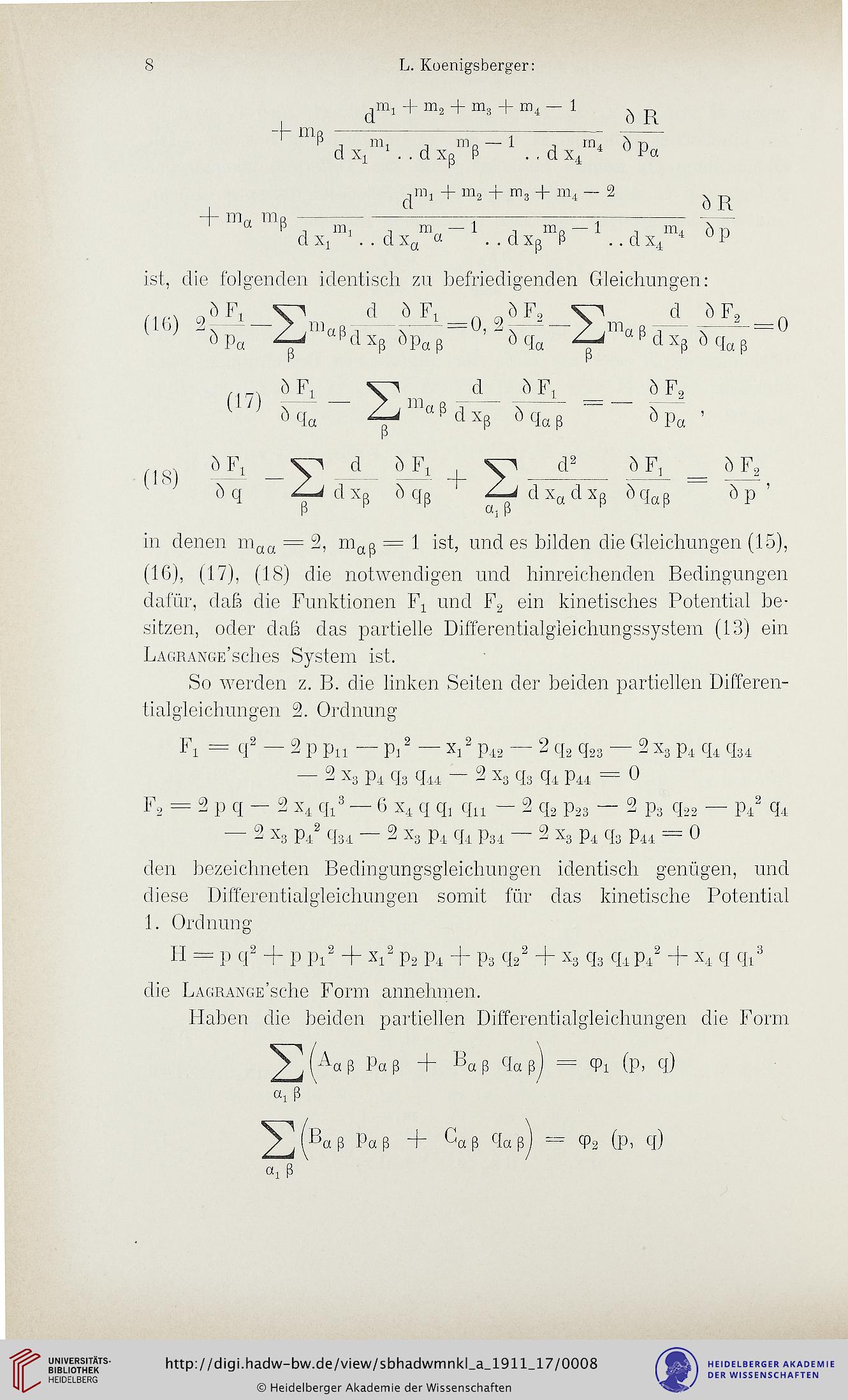Sitzungsberichte der
Heidelberger Akademie der Wissenschaften

L.Koenigsberger:


^mi + m, + in. + m^ — 1
dx/^O.dXß'"ß ^..dxj"^

bR
^Pa

+ ma

+ mg + 11p

dx^

d x.

dxß ß

1 1 m4
..dx.

bR
b p

ist, die folgenden identisch zu befriedigenden Gleichungen:

IG) 2y^
^Pa

-ßcf

d
p^Paß


bF^
^ ha


d b F^
^ß^haß

bF, \ri d^ bF^ _ _ bF,
^ha -^"^'dXß bqcß " bp^ '

(IS)

bF\ \Tl d
^q ß ^Xß

bFi cP
^hß ^ ^dXaCiXß
' a,ß '

^F,
^haß

bF^
b p

in denen m^a = 2, m^ß = 1 ist, und es bilden die Gleichungen (15),
(IG), (17), (18) die notwendigen und hinreichenden Bedingungen
dafür, dah die Funktionen F^ und Fg ein kinetisches Potential be-
sitzen, oder dah das partielle Differentialgleichungssystem (13) ein
LAGRANGE'sches System ist.
So werden z. B. die linken Seilen der beiden partiellen Differen-
tialgleichungen 2. Ordnung

Fi = — 2 p pn — p/ — p,^ — 2 q,g — 2 Xg p^ q^ cjg^
— 2 Xg p^ qg q^^ — 2 Xg qg q., p^ = 0
F, = 2 p q — 2 x^ q^ — 6 x^ q q^ qn — 2 q^ pgg — 2 pg q^ — 1R^ ha
— 2 Xg p^ cpg_ — 2 Xg p^ q^ pg^ — 2 Xg p^ qg p^ = 0

den hezeichneten Bedingungsgleichungen identisch genügen, und
diese Differentialgleichungen somit für das kinetische Potential
1. Ordnung
H = p p p^3 p^ p^ _j_ p^ q^2 ^ ^ ^ ^ q ^3
die LAGRANGE'sche Form annehmen.
Haben die beiden partiellen Differentialgleichungen die Form
^(^aß Paß + Faß qctß) = qF h)
a, ß
fFa ß Pa ß p* ^'a ß ha ßj — Tg (Pi h)
a, ß