DOI Page / Citation link:
https://doi.org/10.11588/diglit.36524#0007
Randwertaufgabe für A(u) = 0.
(A.16)
einfach zusammenhängende Fläche mit ; dabei sollen die
a,,,b„,c,, stückweise analytisch sein, keinen Verzweigungs- und
keinen unendlichfernen Punkt von St enthalten und mit Umlauf-
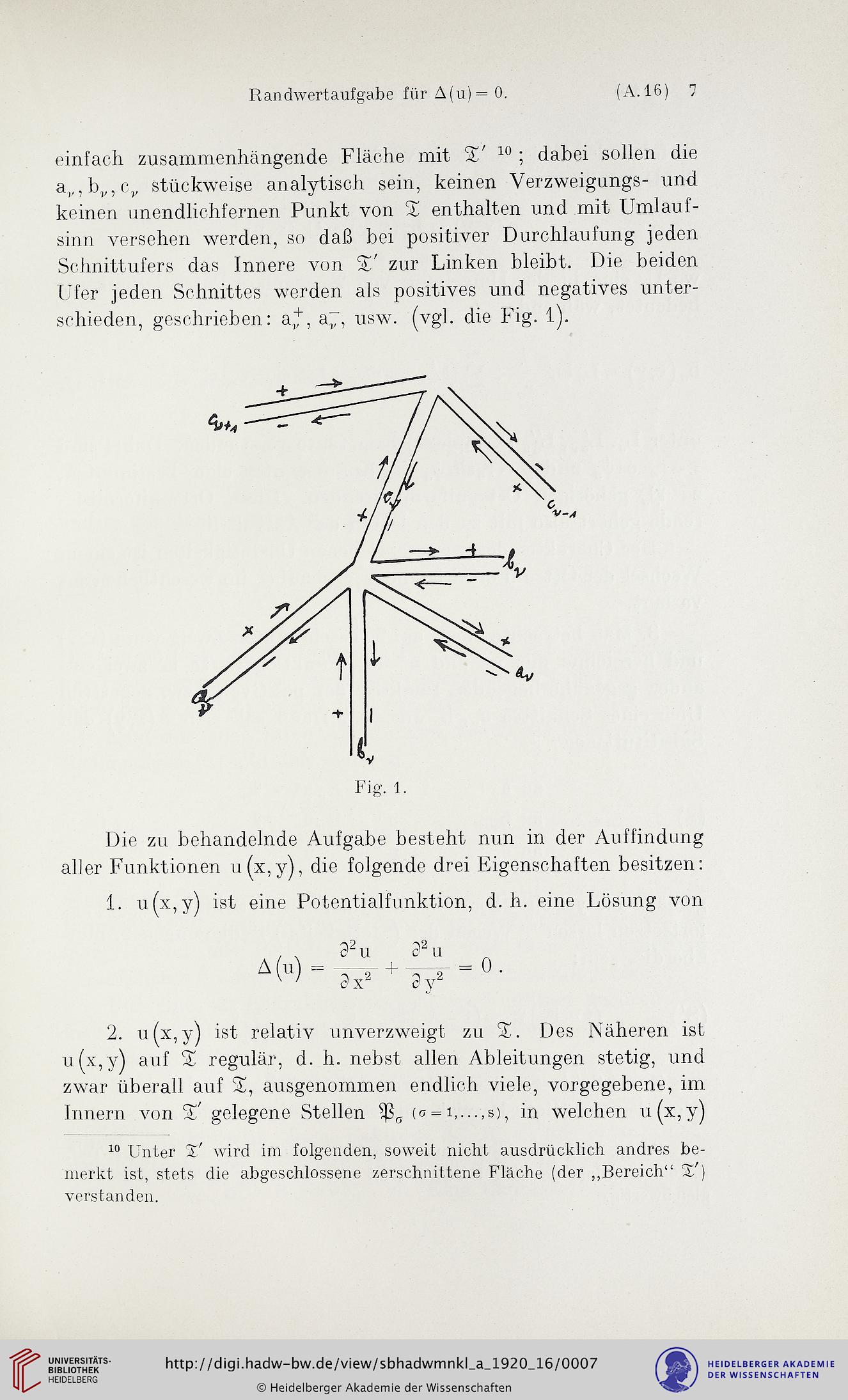
sinn versehen werden, so daß bei positiver Durchlaufung jeden
Schnittufers das Innere von SU zur Linken bleibt. Die beiden
Ufer jeden Schnittes werden als positives und negatives unter-
schieden, geschrieben: aj^, ay, usw. (vgl. die Fig. l).
Die zu behandelnde Aufgabe besteht nun in der Auffindung
aller Funktionen u(x,y), die folgende drei Eigenschaften besitzen:
1. u(x,y) ist eine Potentialfunktion, d. h. eine Lösung von
2. u(x,y) ist relativ unverzweigt zu U. Des Näheren ist
u(x,y) auf St! regulär, d. h. nebst allen Ableitungen stetig, und
zwar überall auf U, ausgenommen endlich viele, vorgegebene, im
Innern von SU gelegene Stellen (<? = i,...,s), in welchen u(x,y)
Unter I' wird im folgenden, soweit nicht ausdrücklich andres be-
merkt ist, stets die abgeschlossene zerschnittene Fläche (der ,,Bereich" U)
verstanden.
(A.16)
einfach zusammenhängende Fläche mit ; dabei sollen die
a,,,b„,c,, stückweise analytisch sein, keinen Verzweigungs- und
keinen unendlichfernen Punkt von St enthalten und mit Umlauf-
sinn versehen werden, so daß bei positiver Durchlaufung jeden
Schnittufers das Innere von SU zur Linken bleibt. Die beiden
Ufer jeden Schnittes werden als positives und negatives unter-
schieden, geschrieben: aj^, ay, usw. (vgl. die Fig. l).
Die zu behandelnde Aufgabe besteht nun in der Auffindung
aller Funktionen u(x,y), die folgende drei Eigenschaften besitzen:
1. u(x,y) ist eine Potentialfunktion, d. h. eine Lösung von
2. u(x,y) ist relativ unverzweigt zu U. Des Näheren ist
u(x,y) auf St! regulär, d. h. nebst allen Ableitungen stetig, und
zwar überall auf U, ausgenommen endlich viele, vorgegebene, im
Innern von SU gelegene Stellen (<? = i,...,s), in welchen u(x,y)
Unter I' wird im folgenden, soweit nicht ausdrücklich andres be-
merkt ist, stets die abgeschlossene zerschnittene Fläche (der ,,Bereich" U)
verstanden.