DOI Page / Citation link:
https://doi.org/10.11588/diglit.43850#0004
4
Ernst Roeser:
Der Beweis soll so geführt werden, daß der Ansatz gemacht wird:
sh a
sh c
sin f(2).
eck
0
wird yj Parallelwinkel
von
sh r
— X
e
Läßt man
y, also:
(3)
zeigen, daß f(2)=2 ist. Es wäre also im Drei-
. „ sh(r-J
sm fW = —
ins Unendliche rücken, so
Nun ist, wie bekannt ist1),
(4) e® = chy und daraus:
(5) s = S • sh y,
wobei S eine Konstante ist. Also aus 3 und 4:
sin f(77(2/)) -
ch?/
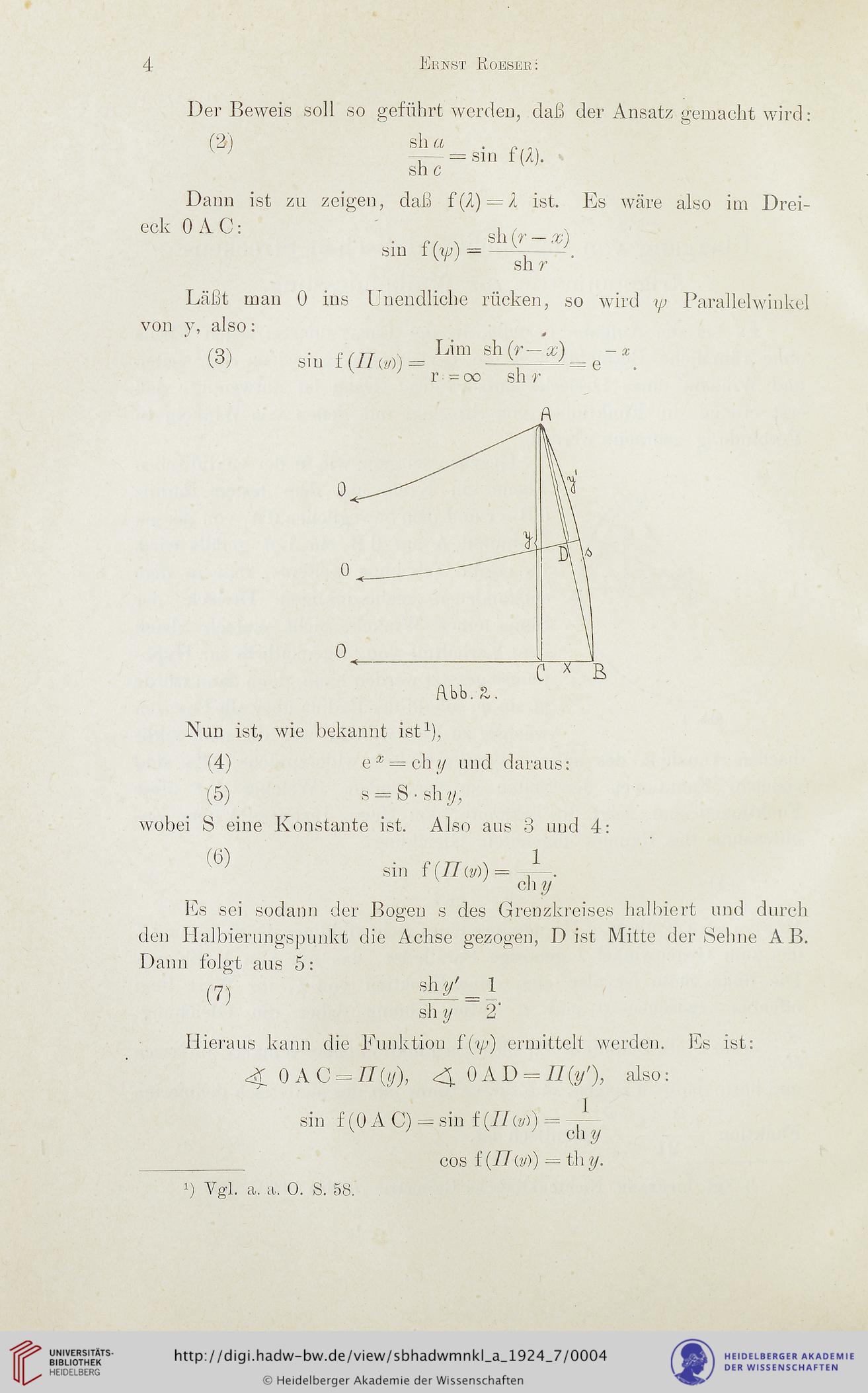
Es sei sodann der Bogen s des Grenzkreises halbiert und durch
den Halbierungspunkt die Achse gezogen, D ist Mitte der Sehne AB.
Dann folgt aus 5:
m sh y' _1
shy 2'
Hieraus kann die Funktion f(y?) ermittelt werden. Es ist:
0 A C = 27 (y), PI 0 A D = 27(/), also:
sin f (0 A C) = sin f (77 (//)) =
_ cos f (77 (?/)) = th y.
■) Vgl. a. a. 0. S. 58.
Ernst Roeser:
Der Beweis soll so geführt werden, daß der Ansatz gemacht wird:
sh a
sh c
sin f(2).
eck
0
wird yj Parallelwinkel
von
sh r
— X
e
Läßt man
y, also:
(3)
zeigen, daß f(2)=2 ist. Es wäre also im Drei-
. „ sh(r-J
sm fW = —
ins Unendliche rücken, so
Nun ist, wie bekannt ist1),
(4) e® = chy und daraus:
(5) s = S • sh y,
wobei S eine Konstante ist. Also aus 3 und 4:
sin f(77(2/)) -
ch?/
Es sei sodann der Bogen s des Grenzkreises halbiert und durch
den Halbierungspunkt die Achse gezogen, D ist Mitte der Sehne AB.
Dann folgt aus 5:
m sh y' _1
shy 2'
Hieraus kann die Funktion f(y?) ermittelt werden. Es ist:
0 A C = 27 (y), PI 0 A D = 27(/), also:
sin f (0 A C) = sin f (77 (//)) =
_ cos f (77 (?/)) = th y.
■) Vgl. a. a. 0. S. 58.