8
Ernst Roeser
§2.
Die Konstruktion im Falle imaginärer Winkel.
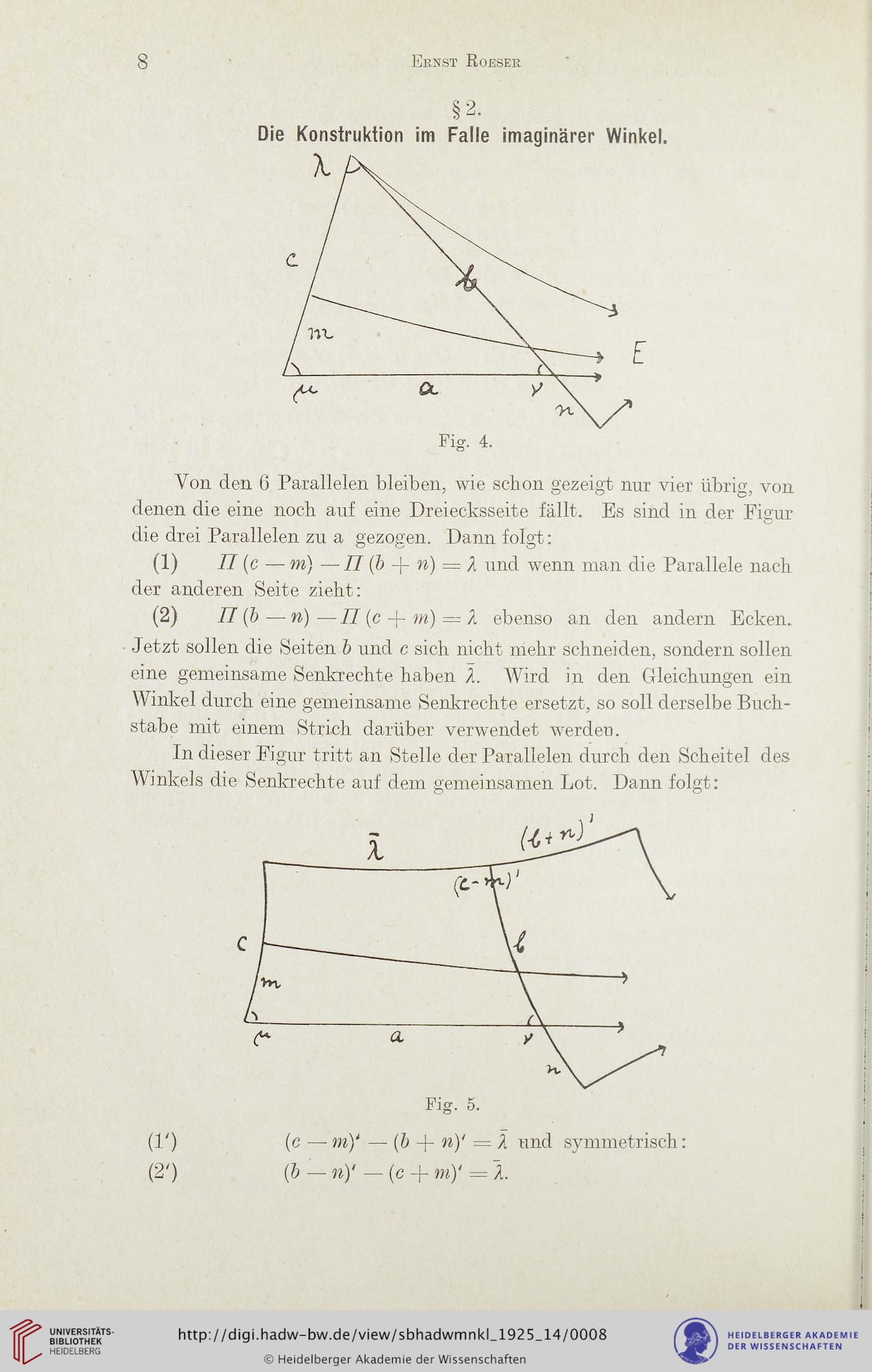
Von den 6 Parallelen bleiben, wie schon gezeigt nur vier übrig, von
denen die eine noch auf eine Dreiecksseite fällt. Es sind in der Figur
die drei Parallelen zu a gezogen. Dann folgt:
(1) n (c — m) —II (& 4~ w) = un(l wenn man die Parallele nach
der anderen Seite zieht:
(2) II (b — n) —II (c + = % ebenso an den andern Ecken.
Jetzt sollen die Seiten b und c sich nicht mehr schneiden, sondern sollen
eine gemeinsame Senkrechte haben Ä. Wird in den Gleichungen ein
Winkel durch eine gemeinsame Senkrechte ersetzt, so soll derselbe Buch-
stabe mit einem Strich darüber verwendet werden.
In dieser Figur tritt an Stelle der Parallelen durch den Scheitel des
Winkels die Senkrechte auf dem gemeinsamen Lot. Dann folgt:
(1') (c — m)1 — (ö + n)' = A und symmetrisch:
(2') (b—n)'—(c-\-my=~Ä.
Ernst Roeser
§2.
Die Konstruktion im Falle imaginärer Winkel.
Von den 6 Parallelen bleiben, wie schon gezeigt nur vier übrig, von
denen die eine noch auf eine Dreiecksseite fällt. Es sind in der Figur
die drei Parallelen zu a gezogen. Dann folgt:
(1) n (c — m) —II (& 4~ w) = un(l wenn man die Parallele nach
der anderen Seite zieht:
(2) II (b — n) —II (c + = % ebenso an den andern Ecken.
Jetzt sollen die Seiten b und c sich nicht mehr schneiden, sondern sollen
eine gemeinsame Senkrechte haben Ä. Wird in den Gleichungen ein
Winkel durch eine gemeinsame Senkrechte ersetzt, so soll derselbe Buch-
stabe mit einem Strich darüber verwendet werden.
In dieser Figur tritt an Stelle der Parallelen durch den Scheitel des
Winkels die Senkrechte auf dem gemeinsamen Lot. Dann folgt:
(1') (c — m)1 — (ö + n)' = A und symmetrisch:
(2') (b—n)'—(c-\-my=~Ä.