10
Ernst Roeser
U") (b — ny + (c 4- yy = l
Darauf die Parallelen nach rechts:
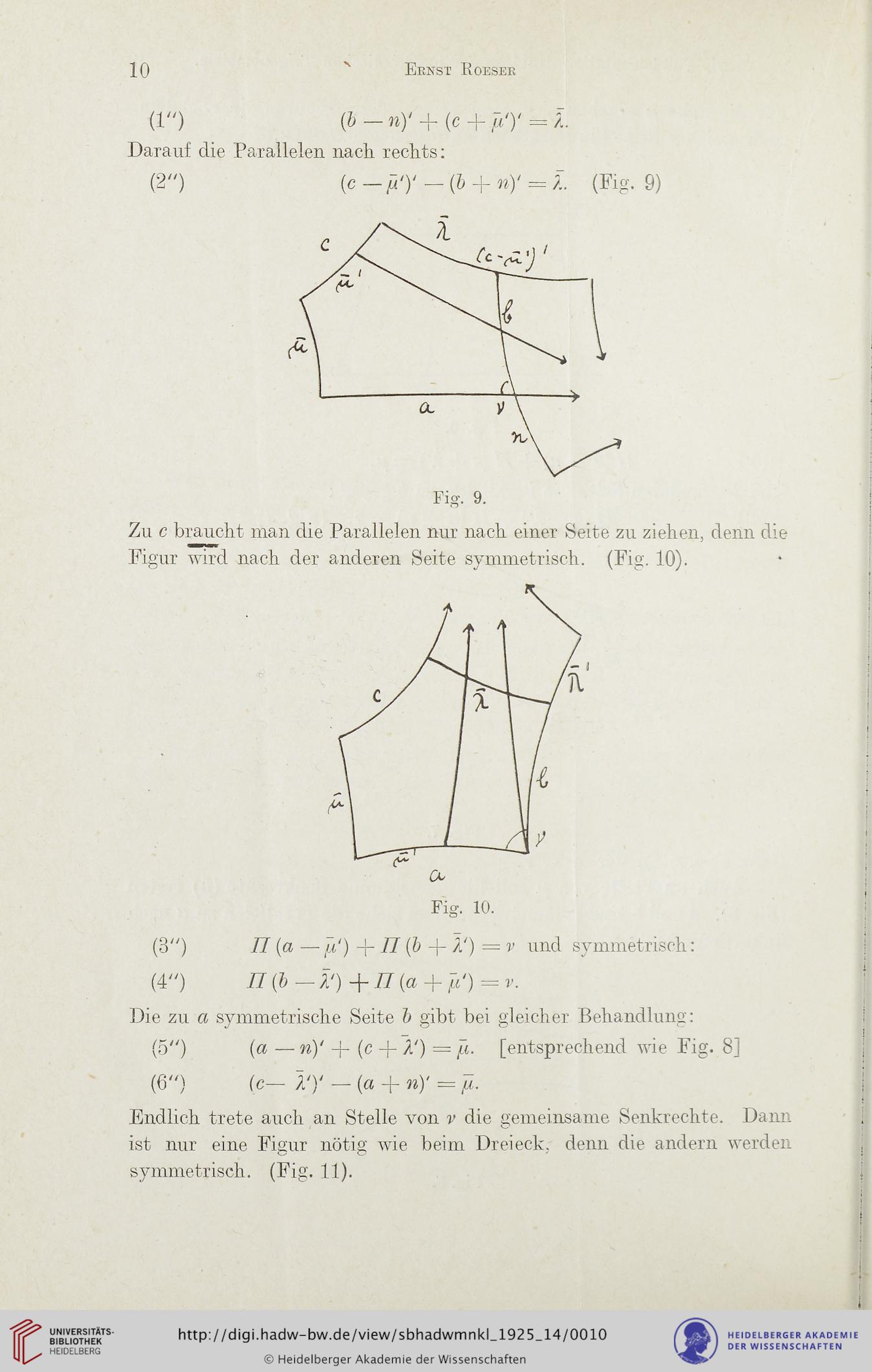
(2") (c — ycy — (b + ny = z. (Fig. 9)
Zu c braucht man die Parallelen nur nach einer Seite zu ziehen, denn die
Figur wird nach der anderen Seite symmetrisch. (Fig. 10).
(3") n (u —/.?) 4- II (b 4- z') = v und symmetrisch:
(4") n (b — Ä') 4~ n (a 4- /?) = v.
Die zu a symmetrische Seite b gibt bei gleicher Behandlung:
(5") (a —ny 4- (c + A') = /h [entsprechend wie Fig. 8]
(6") (c— Ä')' — («4- n)' = y.
Endlich trete auch an Stelle von v die gemeinsame Senkrechte. Dann
ist nur eine Figur nötig wie beim Dreieck, denn die andern werden
symmetrisch. (Fig. 11).
Ernst Roeser
U") (b — ny + (c 4- yy = l
Darauf die Parallelen nach rechts:
(2") (c — ycy — (b + ny = z. (Fig. 9)
Zu c braucht man die Parallelen nur nach einer Seite zu ziehen, denn die
Figur wird nach der anderen Seite symmetrisch. (Fig. 10).
(3") n (u —/.?) 4- II (b 4- z') = v und symmetrisch:
(4") n (b — Ä') 4~ n (a 4- /?) = v.
Die zu a symmetrische Seite b gibt bei gleicher Behandlung:
(5") (a —ny 4- (c + A') = /h [entsprechend wie Fig. 8]
(6") (c— Ä')' — («4- n)' = y.
Endlich trete auch an Stelle von v die gemeinsame Senkrechte. Dann
ist nur eine Figur nötig wie beim Dreieck, denn die andern werden
symmetrisch. (Fig. 11).