Die Fundamentalkonstruktion der hyperbolischen Trigonometrie.
13
EK CE-CK
W GF~ GF
HJ HJ
DK~DCjCK
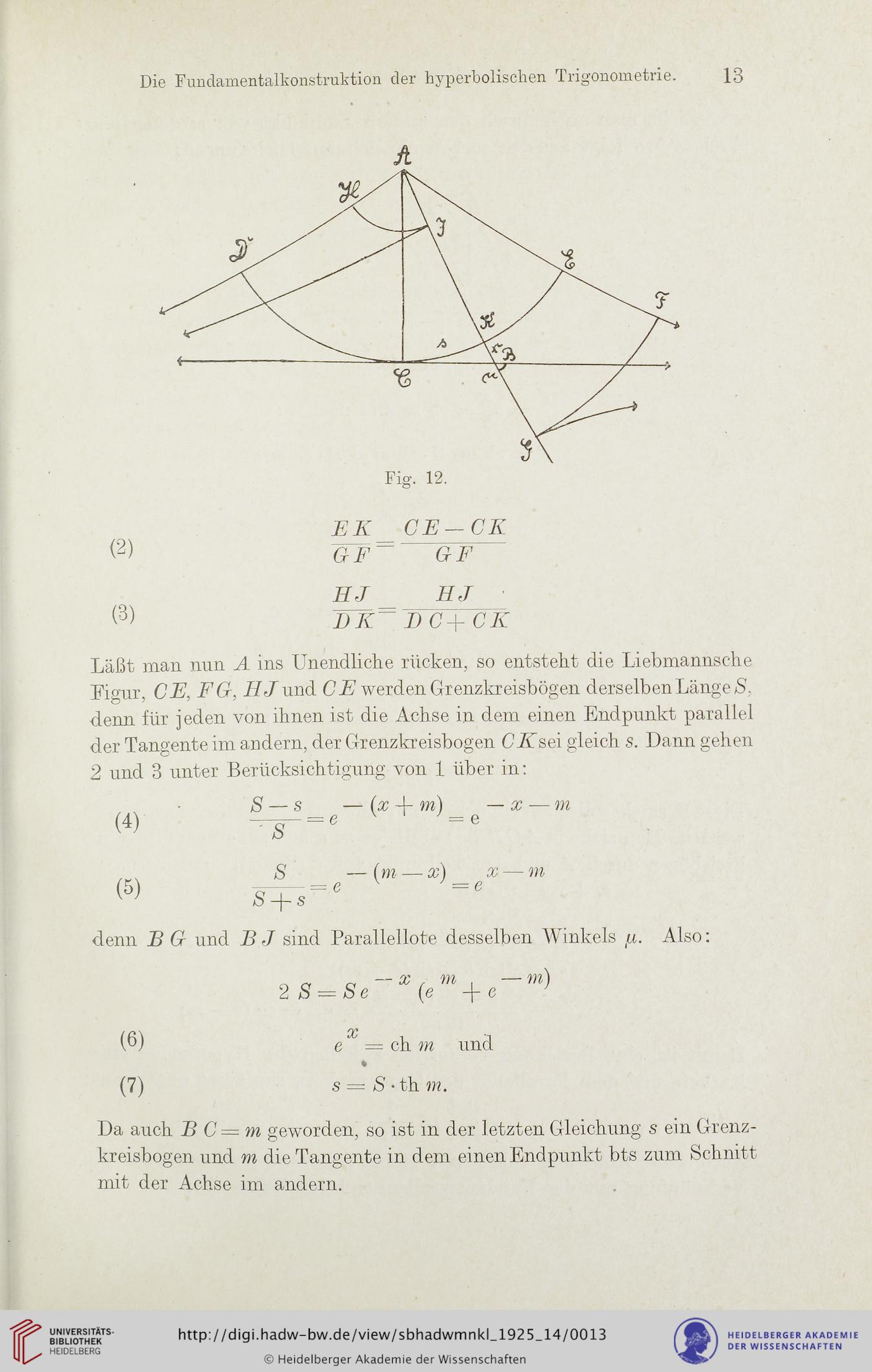
Läßt man nun A ins Unendliche rücken, so entsteht die Liebmannsche
Figur, CE, EG, HJ und CE werden Grenzkreisbögen derselben Länge S.
denn für jeden von ihnen ist die Achse in dem einen Endpunkt parallel
der Tangente im andern, der Grenzkreisbogen CK sei gleich s. Dann gehen
2 und 3 unter Berücksichtigung von 1 über in:
, x ■ S — s — (x 4- m) — x — m
(4) = e
denn B G und B J sind Parallel lote desselben Winkels (u. Also:
o a q “ x ( m i “'w)
2 S = S e (e J- e
(6) eX = ch m und
(7) s=S-thm.
Da auch B C=m geworden, so ist in der letzten Gleichung s ein Grenz-
kreisbogen und m die Tangente in dem einen Endpunkt bts zum Schnitt
mit der Achse im andern.
13
EK CE-CK
W GF~ GF
HJ HJ
DK~DCjCK
Läßt man nun A ins Unendliche rücken, so entsteht die Liebmannsche
Figur, CE, EG, HJ und CE werden Grenzkreisbögen derselben Länge S.
denn für jeden von ihnen ist die Achse in dem einen Endpunkt parallel
der Tangente im andern, der Grenzkreisbogen CK sei gleich s. Dann gehen
2 und 3 unter Berücksichtigung von 1 über in:
, x ■ S — s — (x 4- m) — x — m
(4) = e
denn B G und B J sind Parallel lote desselben Winkels (u. Also:
o a q “ x ( m i “'w)
2 S = S e (e J- e
(6) eX = ch m und
(7) s=S-thm.
Da auch B C=m geworden, so ist in der letzten Gleichung s ein Grenz-
kreisbogen und m die Tangente in dem einen Endpunkt bts zum Schnitt
mit der Achse im andern.