Die komplementären Figuren der nichteuklidischen Ebene.
9
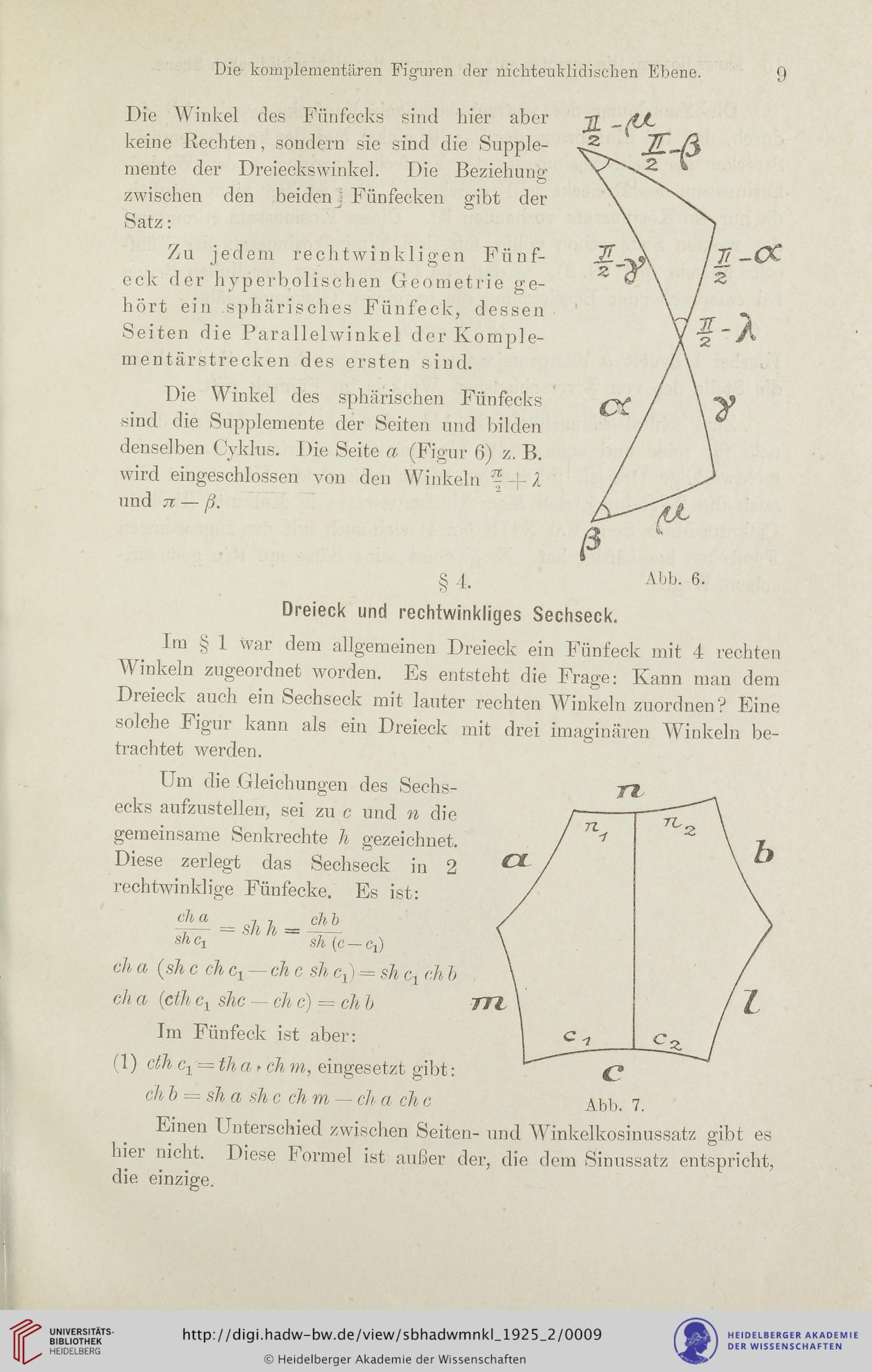
Die Winkel des Fünfecks sind hier aber
keine Rechten, sondern sie sind die Supple-
mente der Dreieckswinke]. Die Beziehung
zwischen den beiden] Fünfecken gibt der
Satz:
Zu jedem rechtwinkligen Fünf-
eck der hyperbolischen Geometrie ge-
hört ein sphärisches Fünfeck, dessen
Seiten die Parallelwinkel der Komple-
mentärstrecken des ersten sind.
Die Winkel des sphärischen Fünfecks
sind die Supplemente der Seiten und bilden
denselben Cyklus. Die Seite a (Figur 6) z. B.
wird eingeschlossen von den Winkeln 2
und 7t — ß.
Dreieck und rechtwinkliges Sechseck.
Im § 1 war dem allgemeinen Dreieck ein Fünfeck mit 4 rechten
Winkeln zugeordnet worden. Es entsteht die Frage: Kann man dem
Dreieck auch ein Sechseck mit lauter rechten Winkeln zuordnen? Eine
solche Figur kann als ein Dreieck mit drei imaginären Winkeln be-
trachtet werden.
Um die Gleichungen des Sechs-
ecks aufzustellen, sei zu c und n die
gemeinsame Senkrechte h gezeichnet.
Diese zerlegt das Sechseck in 2
rechtwinklige Fünfecke. Es ist:
db cl 7 7 cT?»
ch a (shc chcx — ch c sh eß) = sh cx ch b
eh a (eth c} shc — eh c) = ch b
Im Fünfeck ist aber:
(1) eth cx = th a r ch m, eingesetzt gibt:
ch b = sha sh c chm — ch a ch c
C
Abb. 7.
Einen Unterschied zwischen Seiten- und Winkelkosinussatz gibt es
hier nicht. Diese Formel ist außer der, die dem Sinussatz entspricht,
die einzige.
9
Die Winkel des Fünfecks sind hier aber
keine Rechten, sondern sie sind die Supple-
mente der Dreieckswinke]. Die Beziehung
zwischen den beiden] Fünfecken gibt der
Satz:
Zu jedem rechtwinkligen Fünf-
eck der hyperbolischen Geometrie ge-
hört ein sphärisches Fünfeck, dessen
Seiten die Parallelwinkel der Komple-
mentärstrecken des ersten sind.
Die Winkel des sphärischen Fünfecks
sind die Supplemente der Seiten und bilden
denselben Cyklus. Die Seite a (Figur 6) z. B.
wird eingeschlossen von den Winkeln 2
und 7t — ß.
Dreieck und rechtwinkliges Sechseck.
Im § 1 war dem allgemeinen Dreieck ein Fünfeck mit 4 rechten
Winkeln zugeordnet worden. Es entsteht die Frage: Kann man dem
Dreieck auch ein Sechseck mit lauter rechten Winkeln zuordnen? Eine
solche Figur kann als ein Dreieck mit drei imaginären Winkeln be-
trachtet werden.
Um die Gleichungen des Sechs-
ecks aufzustellen, sei zu c und n die
gemeinsame Senkrechte h gezeichnet.
Diese zerlegt das Sechseck in 2
rechtwinklige Fünfecke. Es ist:
db cl 7 7 cT?»
ch a (shc chcx — ch c sh eß) = sh cx ch b
eh a (eth c} shc — eh c) = ch b
Im Fünfeck ist aber:
(1) eth cx = th a r ch m, eingesetzt gibt:
ch b = sha sh c chm — ch a ch c
C
Abb. 7.
Einen Unterschied zwischen Seiten- und Winkelkosinussatz gibt es
hier nicht. Diese Formel ist außer der, die dem Sinussatz entspricht,
die einzige.