Komplementäre Körper der beiden nichteuklidischen Geometrien.
5
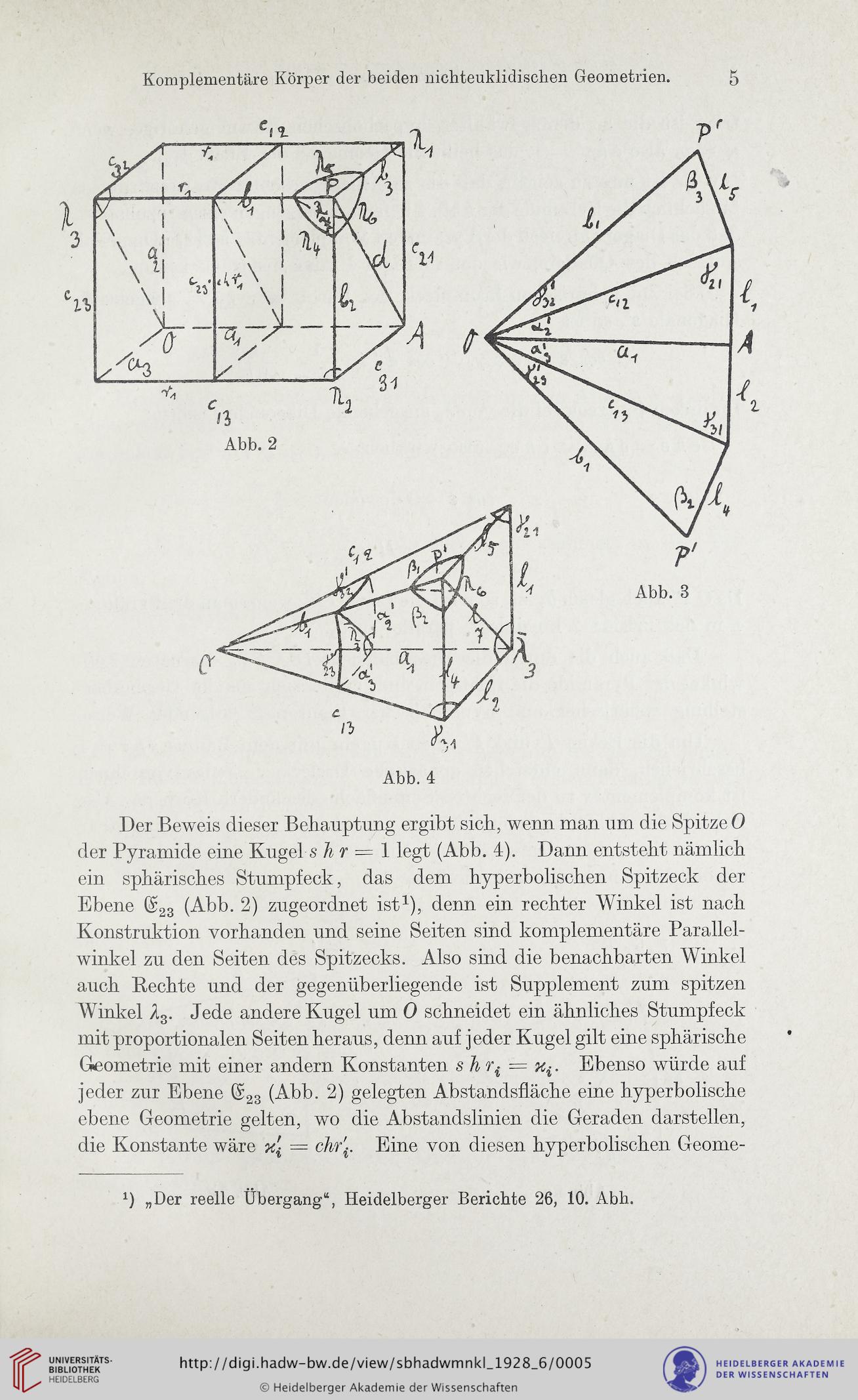
Abb. 4
Der Beweis dieser Behauptung ergibt sich, wenn man um die Spitze 0
der Pyramide eine Kugel s h r — 1 legt (Abb. 4). Dann entsteht nämlich
ein sphärisches Stumpfeck, das dem hyperbolischen Spitzeck der
Ebene @23 (Abb. 2) zugeordnet ist1), denn ein rechter Winkel ist nach
Konstruktion vorhanden und seine Seiten sind komplementäre Parallel-
winkel zu den Seiten des Spitzecks. Also sind die benachbarten Winkel
auch Rechte und der gegenüberliegende ist Supplement zum spitzen
Winkel z3. Jede andere Kugel um 0 schneidet ein ähnliches Stumpf eck
mit proportionalen Seiten heraus, denn auf jeder Kugel gilt eine sphärische
Geometrie mit einer andern Konstanten shri = . Ebenso würde auf
jeder zur Ebene @23 (Abb. 2) gelegten Abstandsfläche eine hyperbolische
ebene Geometrie gelten, wo die Abstandslinien die Geraden darstellen,
die Konstante wäre = chr^. Eine von diesen hyperbolischen Geome-
„Der reelle Übergang“, Heidelberger Berichte 26, 10. Abh.
5
Abb. 4
Der Beweis dieser Behauptung ergibt sich, wenn man um die Spitze 0
der Pyramide eine Kugel s h r — 1 legt (Abb. 4). Dann entsteht nämlich
ein sphärisches Stumpfeck, das dem hyperbolischen Spitzeck der
Ebene @23 (Abb. 2) zugeordnet ist1), denn ein rechter Winkel ist nach
Konstruktion vorhanden und seine Seiten sind komplementäre Parallel-
winkel zu den Seiten des Spitzecks. Also sind die benachbarten Winkel
auch Rechte und der gegenüberliegende ist Supplement zum spitzen
Winkel z3. Jede andere Kugel um 0 schneidet ein ähnliches Stumpf eck
mit proportionalen Seiten heraus, denn auf jeder Kugel gilt eine sphärische
Geometrie mit einer andern Konstanten shri = . Ebenso würde auf
jeder zur Ebene @23 (Abb. 2) gelegten Abstandsfläche eine hyperbolische
ebene Geometrie gelten, wo die Abstandslinien die Geraden darstellen,
die Konstante wäre = chr^. Eine von diesen hyperbolischen Geome-
„Der reelle Übergang“, Heidelberger Berichte 26, 10. Abh.