Komplementäre Körper der beiden nicliteuklidiscben Geometrien.
9
in der oben zitierten Abhandlung vom reellen Übergang. Die Richtig-
keit läßt sich sofort wieder mit Hilfe der Formeln nachprüfen. Zu der
Abbildung 3 bestimmen wir auf diese Weise die entsprechende sphärische
und setzen sie auch zu einer Pyramide zusammen. Die Ebenen zweier
Dreiecke mögen wieder einen rechten Winkel bilden, so sind die andern
Winkel bestimmt, weil das durch die Kugel herausgeschnittene 4 Eck
bestimmt ist (4 Seiten, ein Winkel).
Um P' die Spitze der Pyramide sei wieder eine Kugel gelegt, der
Radius sei denn dann messen die Bogen gerade die Seiten der körper-
lichen Ecke P'. Das so entstehende Stumpf eck, das auch die linke Seite
des Quaders 9, bildet ist zugeordnet dem rechten Spitzeck (Seitenfläche)
des Quaders 2. Betrachten wir die Quader 2 und 9 der beiden Geometrien,
so sehen wir die gegenüberliegenden Seitenflächen miteinander ver-
tauscht und in den Flächen wieder die Seiten, so daß jede Kante mit
der gegenüberliegenden vertauscht ist.
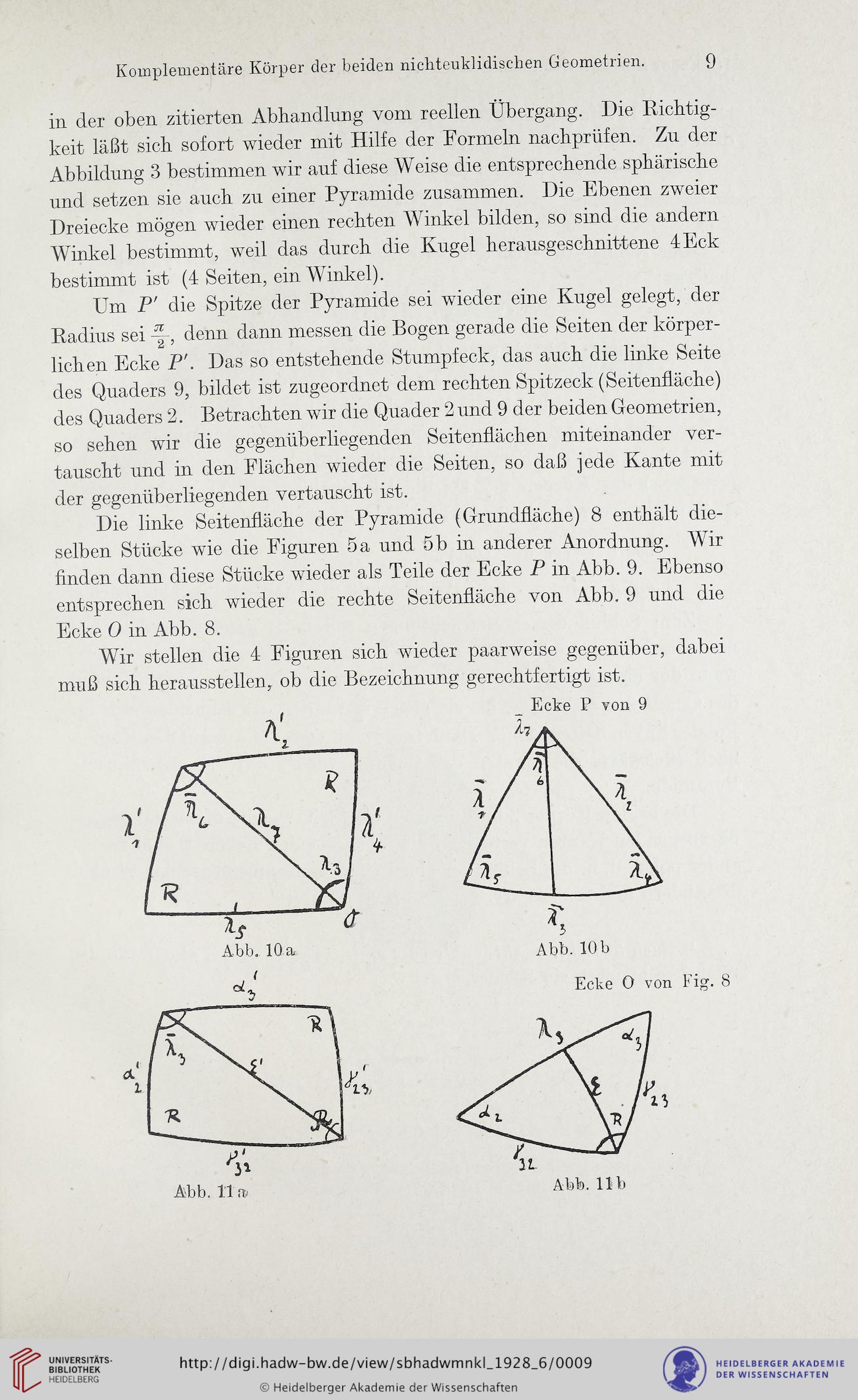
Die linke Seitenfläche der Pyramide (Grundfläche) 8 enthält die-
selben Stücke wie die Figuren 5a und 5b in anderer Anordnung. Wir
finden dann diese Stücke wieder als Teile der Ecke P in Abb. 9. Ebenso
entsprechen sich wieder die rechte Seitenfläche von Abb. 9 und die
Ecke 0 in Abb. 8.
Wir stellen die 4 Figuren sich wieder paarweise gegenüber, dabei
muß sich herausstellen, ob die Bezeichnung gerechtfertigt ist.
Abb. 11 a
9
in der oben zitierten Abhandlung vom reellen Übergang. Die Richtig-
keit läßt sich sofort wieder mit Hilfe der Formeln nachprüfen. Zu der
Abbildung 3 bestimmen wir auf diese Weise die entsprechende sphärische
und setzen sie auch zu einer Pyramide zusammen. Die Ebenen zweier
Dreiecke mögen wieder einen rechten Winkel bilden, so sind die andern
Winkel bestimmt, weil das durch die Kugel herausgeschnittene 4 Eck
bestimmt ist (4 Seiten, ein Winkel).
Um P' die Spitze der Pyramide sei wieder eine Kugel gelegt, der
Radius sei denn dann messen die Bogen gerade die Seiten der körper-
lichen Ecke P'. Das so entstehende Stumpf eck, das auch die linke Seite
des Quaders 9, bildet ist zugeordnet dem rechten Spitzeck (Seitenfläche)
des Quaders 2. Betrachten wir die Quader 2 und 9 der beiden Geometrien,
so sehen wir die gegenüberliegenden Seitenflächen miteinander ver-
tauscht und in den Flächen wieder die Seiten, so daß jede Kante mit
der gegenüberliegenden vertauscht ist.
Die linke Seitenfläche der Pyramide (Grundfläche) 8 enthält die-
selben Stücke wie die Figuren 5a und 5b in anderer Anordnung. Wir
finden dann diese Stücke wieder als Teile der Ecke P in Abb. 9. Ebenso
entsprechen sich wieder die rechte Seitenfläche von Abb. 9 und die
Ecke 0 in Abb. 8.
Wir stellen die 4 Figuren sich wieder paarweise gegenüber, dabei
muß sich herausstellen, ob die Bezeichnung gerechtfertigt ist.
Abb. 11 a