Sphärische und hyperbolische Vielecke.
11
Da k <
chungen des
1, wird
cos v
cos y
> 1. Es ergeben sich die beiden Glei-
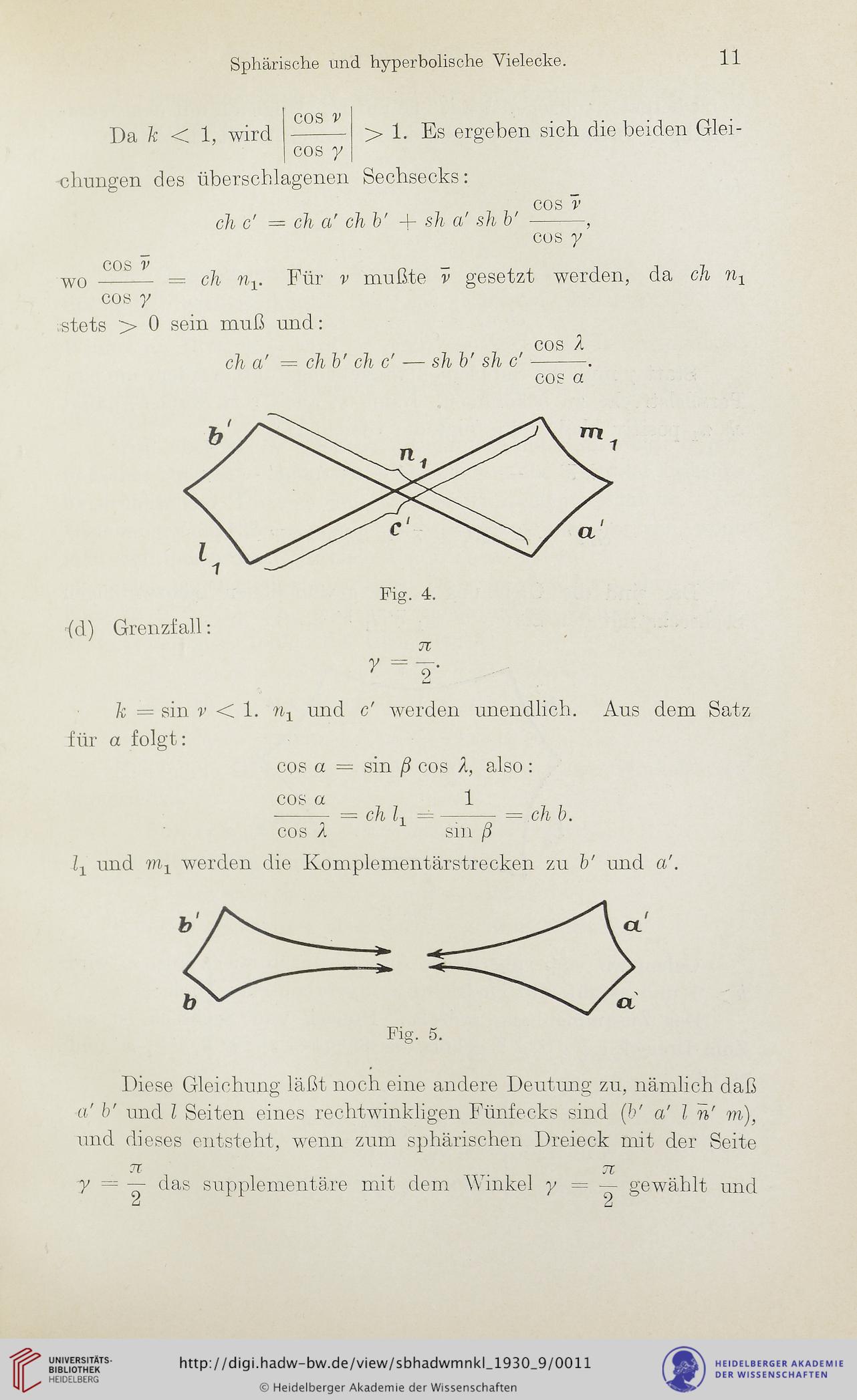
überschlagenen Sechsecks:
ch c' = ch a' ch b' + sh a' sh b'
cos v
cos y’
cos v
wo -
cos y
;stets > 0
— ch nx. Für v mußte v gesetzt werden,
sein muß und:
da ch nx
Id) Grenzfall:
71
k = sin v < 1. nx und c' werden unendlich. Aus dem Satz
für a folgt:
cos a = sin ß cos A, also:
cos a 1
- = chl-L =- — ch b.
cos A sm ß
1-l und mx werden die Komplementärstrecken zu b' und a'.
Diese Gleichung läßt noch eine andere Deutung zu, nämlich daß
a' b' und Z Seiten eines rechtwinkligen Fünfecks sind (Z/ a' Z n' m),
und dieses entsteht, wenn zum sphärischen Dreieck mit der Seite
zr . . zc
7 = — das supplementäre mit dem Winkel y = — gewählt und
2 ■ 2
11
Da k <
chungen des
1, wird
cos v
cos y
> 1. Es ergeben sich die beiden Glei-
überschlagenen Sechsecks:
ch c' = ch a' ch b' + sh a' sh b'
cos v
cos y’
cos v
wo -
cos y
;stets > 0
— ch nx. Für v mußte v gesetzt werden,
sein muß und:
da ch nx
Id) Grenzfall:
71
k = sin v < 1. nx und c' werden unendlich. Aus dem Satz
für a folgt:
cos a = sin ß cos A, also:
cos a 1
- = chl-L =- — ch b.
cos A sm ß
1-l und mx werden die Komplementärstrecken zu b' und a'.
Diese Gleichung läßt noch eine andere Deutung zu, nämlich daß
a' b' und Z Seiten eines rechtwinkligen Fünfecks sind (Z/ a' Z n' m),
und dieses entsteht, wenn zum sphärischen Dreieck mit der Seite
zr . . zc
7 = — das supplementäre mit dem Winkel y = — gewählt und
2 ■ 2