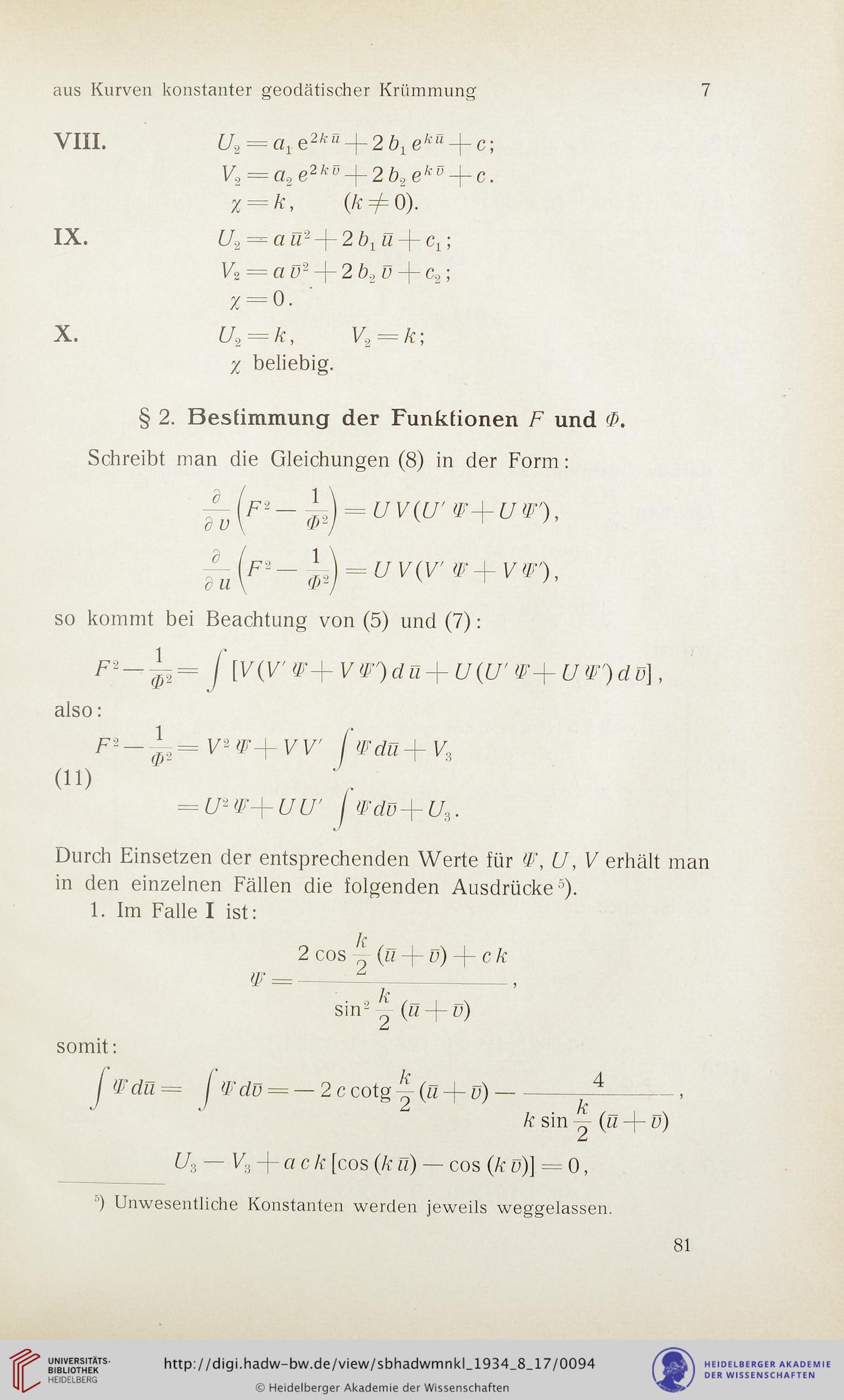DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.43680#0094
aus Kurven konstanter geodätischer Krümmung
7
VIII. t72 = a1.e2/c“ + 2ö1e/cS + c;
V2 = a2 e2ku-^-2b2 eks-^-c.
% = k, (/£#=0)-
IX. U2 = ci u,2 —1~ 2 b u —p ;
V2 = ci v2 -j- 2 b.> D + c2;
% = 0. '
X. U2 = k, V2 = k;
% beliebig.
§ 2. Bestimmung der Funktionen F und k.
Schreibt man die Gleichungen (8) in der Form:
aT (/?2 ~^ = uv(u' ®'+ u >F} ’
(fä ~^) = u v{y’ + v•
so kommt bei Beachtung von (5) und (7):
F2 — ~ = I [V(V W+VW')dü + lJ(JJ' W+UW'jdD],
also:
F2—~ = V2 VV' j F du + V3
(11) '/•
= U2W+UU' Vdv+U3.
Durch Einsetzen der entsprechenden Werte für F, U, V erhält man
in den einzelnen Fällen die folgenden Ausdrücke5).
1. Im Falle I ist:
/r
2 cos (ä + ü)-]- c k
F =-—-,
sin2 (w + D)
somit:
lFdü = lFdü =— 2 c cotg (ü “F ü)-->
k sin — (ü-\-u)
U3 — V3-\-ac k [cos (/r z7) — cos (k ü)] = 0,
°) Unwesentliche Konstanten werden jeweils weggelassen.
81
7
VIII. t72 = a1.e2/c“ + 2ö1e/cS + c;
V2 = a2 e2ku-^-2b2 eks-^-c.
% = k, (/£#=0)-
IX. U2 = ci u,2 —1~ 2 b u —p ;
V2 = ci v2 -j- 2 b.> D + c2;
% = 0. '
X. U2 = k, V2 = k;
% beliebig.
§ 2. Bestimmung der Funktionen F und k.
Schreibt man die Gleichungen (8) in der Form:
aT (/?2 ~^ = uv(u' ®'+ u >F} ’
(fä ~^) = u v{y’ + v•
so kommt bei Beachtung von (5) und (7):
F2 — ~ = I [V(V W+VW')dü + lJ(JJ' W+UW'jdD],
also:
F2—~ = V2 VV' j F du + V3
(11) '/•
= U2W+UU' Vdv+U3.
Durch Einsetzen der entsprechenden Werte für F, U, V erhält man
in den einzelnen Fällen die folgenden Ausdrücke5).
1. Im Falle I ist:
/r
2 cos (ä + ü)-]- c k
F =-—-,
sin2 (w + D)
somit:
lFdü = lFdü =— 2 c cotg (ü “F ü)-->
k sin — (ü-\-u)
U3 — V3-\-ac k [cos (/r z7) — cos (k ü)] = 0,
°) Unwesentliche Konstanten werden jeweils weggelassen.
81