Ultrakurzwellen
29
und zwar ist
/lOO 703
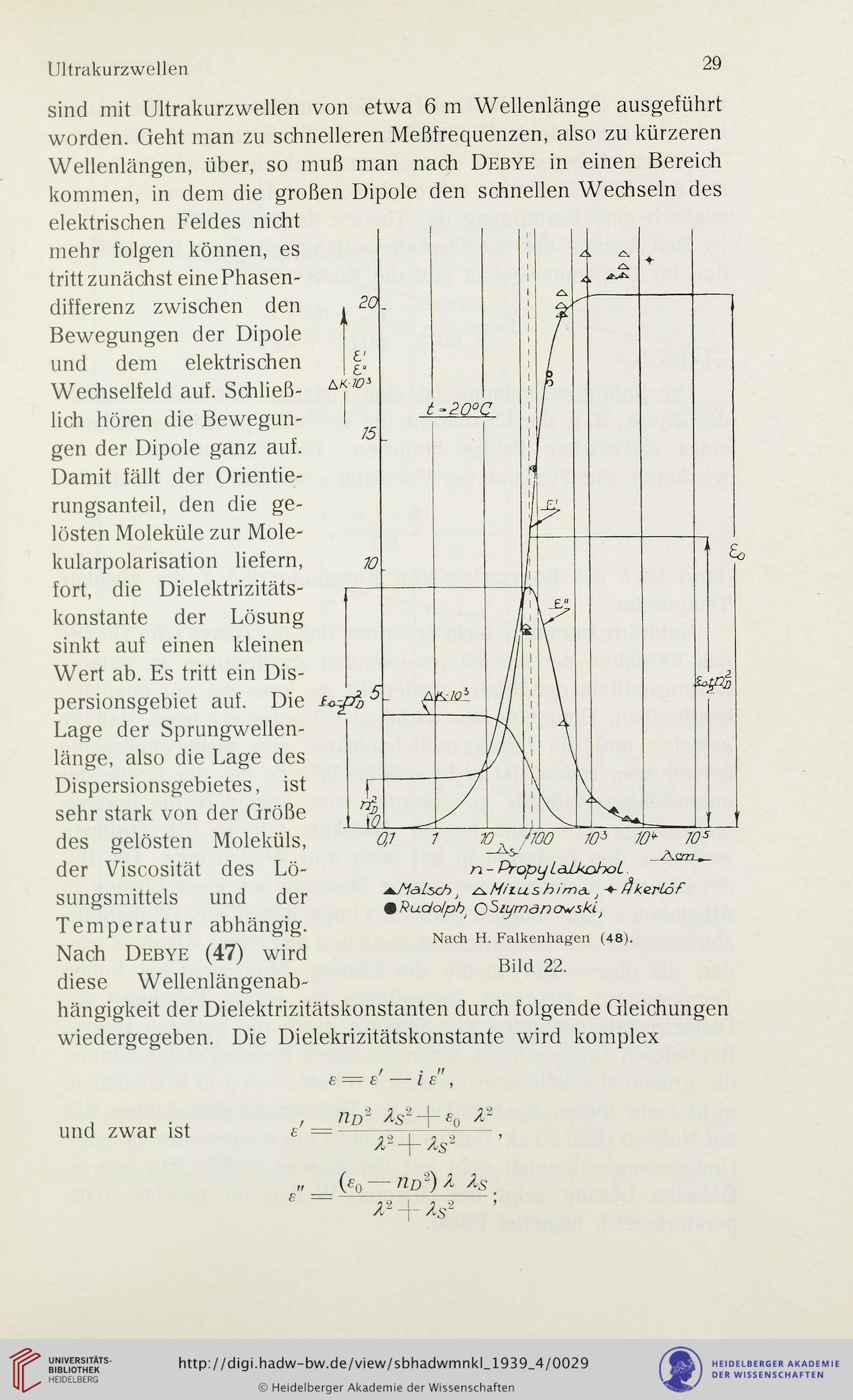
n - Propy L&LkdboL
t zk Mit us h im&. 1 ■*- flkerLöf
QRudo/pp OSiymöncwski.)
Nach H. Falkenhagen (48).
Bild 22.
sind mit Ultrakurzwellen von etwa 6 m Wellenlänge ausgeführt
worden. Geht man zu schnelleren Meßfrequenzen, also zu kürzeren
Wellenlängen, über, so muß man nach Debye in einen Bereich
kommen, in dem die großen Dipole den schnellen Wechseln des
elektrischen Feldes nicht
mehr folgen können, es
tritt zunächst eine Phasen¬
differenz zwischen den
Bewegungen der Dipole
und dem elektrischen
Wechselfeld auf. Schlie߬
lich hören die Bewegun¬
gen der Dipole ganz auf.
Damit fällt der Orientie¬
rungsanteil, den die ge¬
lösten Moleküle zur Mole¬
kularpolarisation liefern,
fort, die Dielektrizitäts¬
konstante der Lösung
sinkt auf einen kleinen
Wert ab. Es tritt ein Dis¬
persionsgebiet auf. Die
Lage der Sprungwellen¬
länge, also die Lage des
Dispersionsgebietes, ist
sehr stark von der Größe
des gelösten Moleküls,
der Viscosität des Lö¬
sungsmittels und der
Temperatur abhängig.
Nach Debye (47) wird
diese Wellenlängenab-
hängigkeit der Dielektrizitätskonstanten durch folgende Gleichungen
wiedergegeben. Die Dielekrizitätskonstante wird komplex
ε = ε' — i ε",
£ - 02 I Ö~2 »
ε
29
und zwar ist
/lOO 703
n - Propy L&LkdboL
t zk Mit us h im&. 1 ■*- flkerLöf
QRudo/pp OSiymöncwski.)
Nach H. Falkenhagen (48).
Bild 22.
sind mit Ultrakurzwellen von etwa 6 m Wellenlänge ausgeführt
worden. Geht man zu schnelleren Meßfrequenzen, also zu kürzeren
Wellenlängen, über, so muß man nach Debye in einen Bereich
kommen, in dem die großen Dipole den schnellen Wechseln des
elektrischen Feldes nicht
mehr folgen können, es
tritt zunächst eine Phasen¬
differenz zwischen den
Bewegungen der Dipole
und dem elektrischen
Wechselfeld auf. Schlie߬
lich hören die Bewegun¬
gen der Dipole ganz auf.
Damit fällt der Orientie¬
rungsanteil, den die ge¬
lösten Moleküle zur Mole¬
kularpolarisation liefern,
fort, die Dielektrizitäts¬
konstante der Lösung
sinkt auf einen kleinen
Wert ab. Es tritt ein Dis¬
persionsgebiet auf. Die
Lage der Sprungwellen¬
länge, also die Lage des
Dispersionsgebietes, ist
sehr stark von der Größe
des gelösten Moleküls,
der Viscosität des Lö¬
sungsmittels und der
Temperatur abhängig.
Nach Debye (47) wird
diese Wellenlängenab-
hängigkeit der Dielektrizitätskonstanten durch folgende Gleichungen
wiedergegeben. Die Dielekrizitätskonstante wird komplex
ε = ε' — i ε",
£ - 02 I Ö~2 »
ε