Oberflächenreaktionen mit Anwendung auf die Winkelverteilung 19
b) J = 2, n = — 1:
<r(02) ~4tt + + 5P2(cos02)) +
+ +2,5 P2(cos02)) +
4* 5,606^ |5'/,)0;2;rf)i;1| • COS^ 0j2.rf x T X
X [cos 6\ • (cos2 02 — * ) — sin cos 02 sin 02) +
F I >
+ 6,865 1 | ‘ COS?’^1)2;<Z)1,1 X
x (cos 6\ • (cos2 02 — ( ) — \ sin sin 02 cos 03);
c) 7 = 1, % = — 4:
er (02) ^4^
J^(cos@^|2
l/il2
F •
— 2,8944 p |5^i0.^1;11 cos epp x 0. dll • cos 012
d) J = 4, n = + 1:
a(02)~4OTw^iM+|(|s;,lil;i,liOp+1 +
4“ ’ 2,0470 (|SA0il;^10| cos^ 0 j. d 10 ~h
+ 1,4144 cos^ x 1;rf x 0) X
X (cos cos 02 — sin 0X sin 02).
(22)
Die Fälle a) und b) enthalten die kleinste Anzahl von Parametern
und wurden daher numerisch untersucht. Die Fig. 4 zeigt den
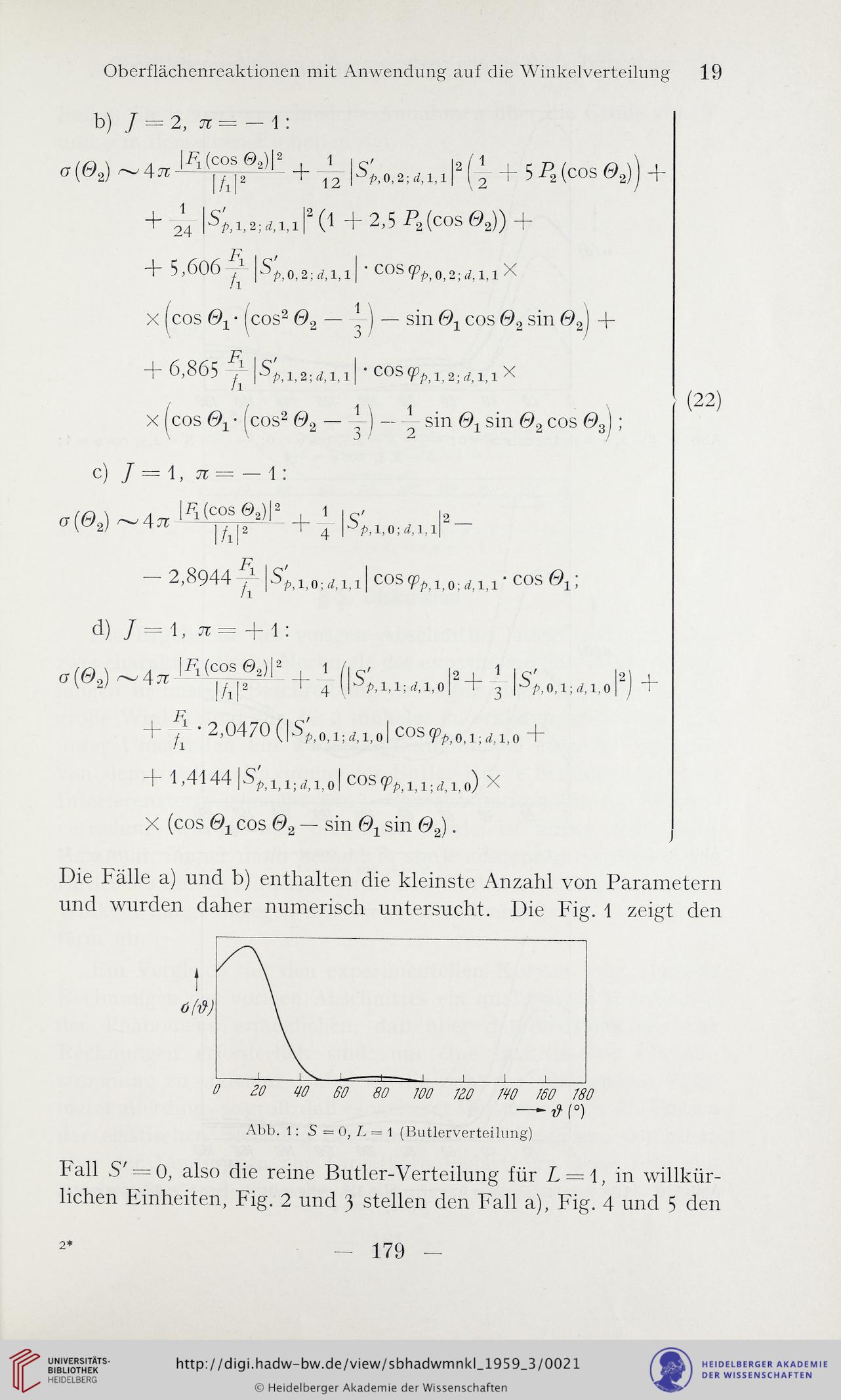
Abb. 1: S = 0, L = 1 (Butlerverteilung)
Fall S' = 0, also die reine Butler-Verteilung für L = 1, in willkür-
lichen Einheiten, Fig. 2 und 3 stellen den Fall a), Fig. 4 und 5 den
2*
179
b) J = 2, n = — 1:
<r(02) ~4tt + + 5P2(cos02)) +
+ +2,5 P2(cos02)) +
4* 5,606^ |5'/,)0;2;rf)i;1| • COS^ 0j2.rf x T X
X [cos 6\ • (cos2 02 — * ) — sin cos 02 sin 02) +
F I >
+ 6,865 1 | ‘ COS?’^1)2;<Z)1,1 X
x (cos 6\ • (cos2 02 — ( ) — \ sin sin 02 cos 03);
c) 7 = 1, % = — 4:
er (02) ^4^
J^(cos@^|2
l/il2
F •
— 2,8944 p |5^i0.^1;11 cos epp x 0. dll • cos 012
d) J = 4, n = + 1:
a(02)~4OTw^iM+|(|s;,lil;i,liOp+1 +
4“ ’ 2,0470 (|SA0il;^10| cos^ 0 j. d 10 ~h
+ 1,4144 cos^ x 1;rf x 0) X
X (cos cos 02 — sin 0X sin 02).
(22)
Die Fälle a) und b) enthalten die kleinste Anzahl von Parametern
und wurden daher numerisch untersucht. Die Fig. 4 zeigt den
Abb. 1: S = 0, L = 1 (Butlerverteilung)
Fall S' = 0, also die reine Butler-Verteilung für L = 1, in willkür-
lichen Einheiten, Fig. 2 und 3 stellen den Fall a), Fig. 4 und 5 den
2*
179