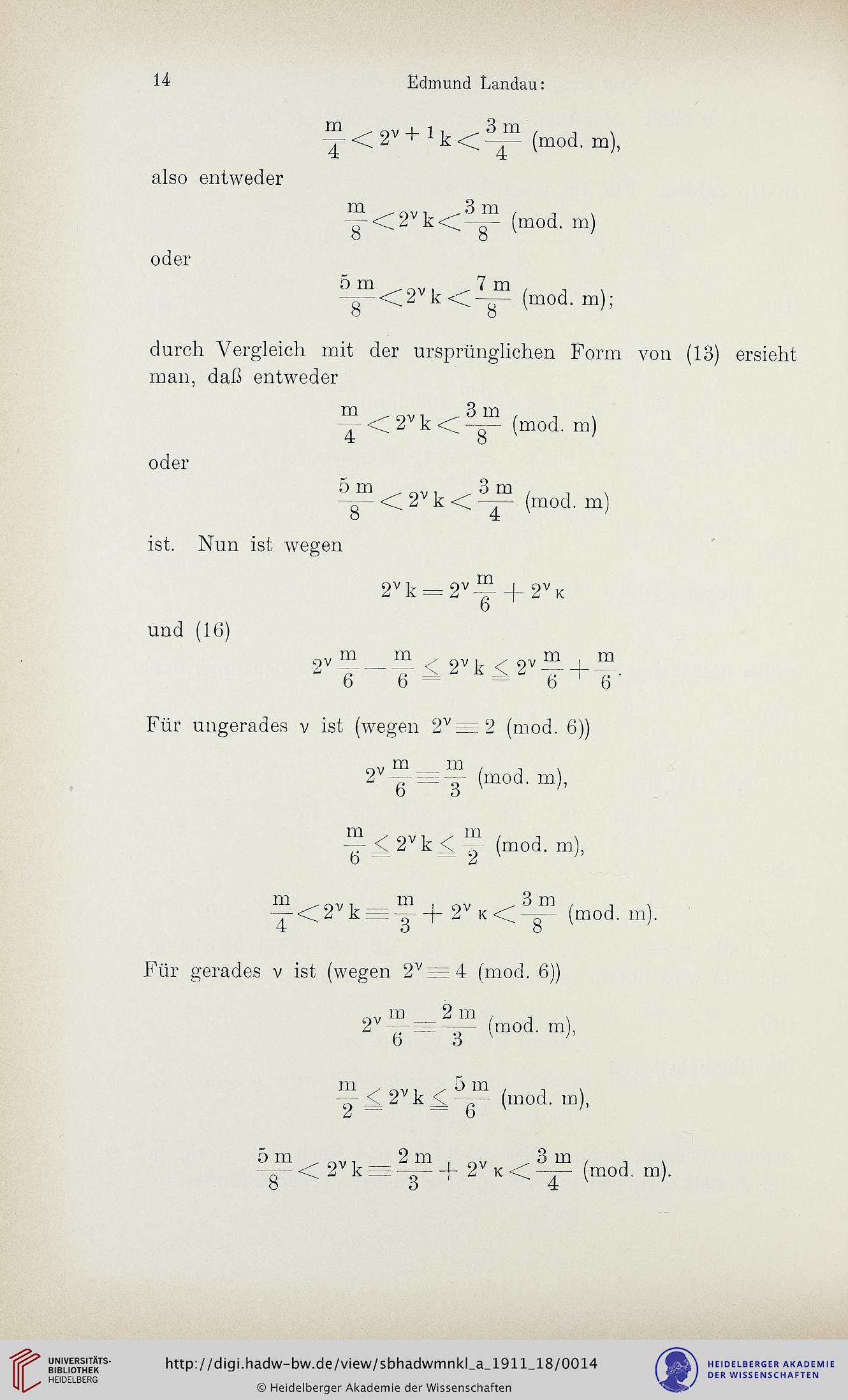14
Edmund Landau:
in
4
<V 2^ + 1 p (mod. m),
also entweder
oder
^<2"k<^ (mod. m)
o o
5m ^7m
^ < 2" k < —- (mod. m);
durch Vergleich mit der ursprünglichen Form von (13) ersieht
man, daß entweder
^ <V 2^ k <V ^ (mod. m)
oder
5m 3m ,
— <V 2 k <V (mod. m)
ist. Nun ist wegen
und (16)
m
2^k = 2^ + 2^K
6
gv .^ < 2"k < 2^- + ^.
b 6 6 b
Für ungerades v ist (wegen 2^-- -2 (mod. 6))
2" ^ L ^ (mod. m),
^ < 2^ k < (mod. m),
b * 2
^< 2" k - y + 2" K < ^ (mod. m).
Für gerades v ist (wegen 2^^r. 4 (mod. 6))
m 2 m
6
(mod. m),
^ ^ ^ (mod. m),
-g - < 2v k -— + 2" K < (mod. m).
Edmund Landau:
in
4
<V 2^ + 1 p (mod. m),
also entweder
oder
^<2"k<^ (mod. m)
o o
5m ^7m
^ < 2" k < —- (mod. m);
durch Vergleich mit der ursprünglichen Form von (13) ersieht
man, daß entweder
^ <V 2^ k <V ^ (mod. m)
oder
5m 3m ,
— <V 2 k <V (mod. m)
ist. Nun ist wegen
und (16)
m
2^k = 2^ + 2^K
6
gv .^ < 2"k < 2^- + ^.
b 6 6 b
Für ungerades v ist (wegen 2^-- -2 (mod. 6))
2" ^ L ^ (mod. m),
^ < 2^ k < (mod. m),
b * 2
^< 2" k - y + 2" K < ^ (mod. m).
Für gerades v ist (wegen 2^^r. 4 (mod. 6))
m 2 m
6
(mod. m),
^ ^ ^ (mod. m),
-g - < 2v k -— + 2" K < (mod. m).