DOI Page / Citation link:
https://doi.org/10.11588/diglit.34795#0019
Frist allographische Fundamentalwinkel der Plagioklase. (A. 13) 19
# W
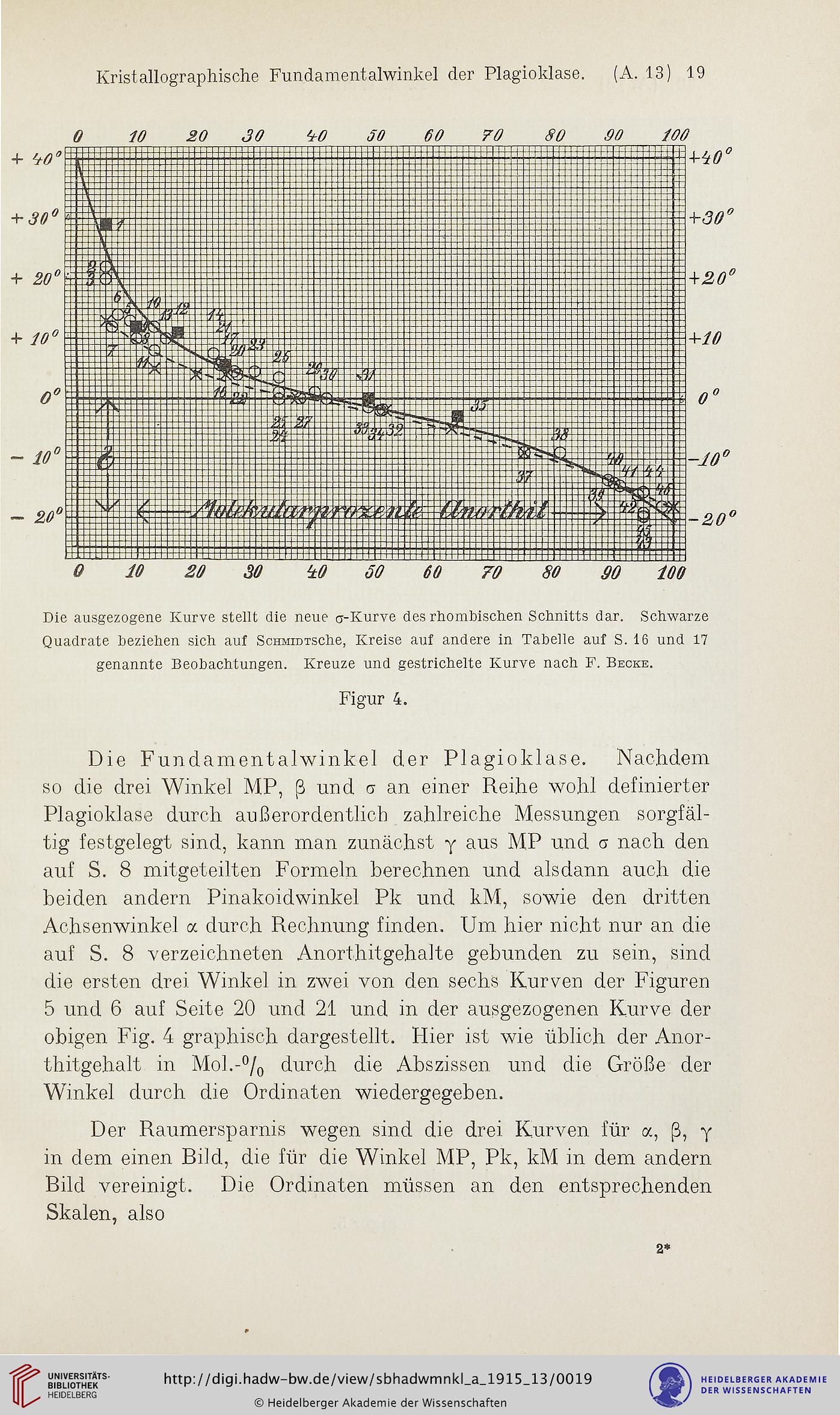
Die ausgezogene Kurve stelit die neue o-Kurve des rhombischen Schnitts dar. Schwarze
Quadrate beziehen sich auf ScHMiDTSche, Kreise auf andere in Tabelle auf S. 16 und 17
genannte Beobachtungen. Kreuze und gestrichelte Kurve nach F. BECKE.
Figur 4.
Die Fundamentalwinkel der Plagioklase. Nachdem
so die drei Winkel MP, ß und o an einer Reihe wohl definierter
Plagioklase durch außerordentlich zahlreiche Messungen sorgfäl-
tig festgelegt sind, kann man zunächst y aus AIP und c nach den
auf S. 8 mitgeteilten Formeln berechnen und alsdann auch die
beiden andern Pinakoidwinkel Pk und kM, sowie den dritten
Achsenwinkel ot durch Rechnung finden. Um hier nicht nur an die
auf S. 8 verzeichneten Anorthitgehalte gebunden zu sein, sind
die ersten drei Winkel in zwei von den sechs Kurven der Figuren
5 und 6 auf Seite 20 und 21 und in der ausgezogenen Kurve der
obigen Fig. 4 graphisch dargestellt. Hier ist wie üblich der Anor-
thitgehalt in Mo].-°/(, durch die Abszissen und die Größe der
Winkel durch die Ordinaten wiedergegeben.
Der Raumersparnis wegen sind die drei Kurven für K, ß, y
in dem einen Bild, die für die Winkel AIP, Pk, kAl in dem andern
Bild vereinigt. Die Ordinaten müssen an den entsprechenden
Skalen, also
2*
# W
Die ausgezogene Kurve stelit die neue o-Kurve des rhombischen Schnitts dar. Schwarze
Quadrate beziehen sich auf ScHMiDTSche, Kreise auf andere in Tabelle auf S. 16 und 17
genannte Beobachtungen. Kreuze und gestrichelte Kurve nach F. BECKE.
Figur 4.
Die Fundamentalwinkel der Plagioklase. Nachdem
so die drei Winkel MP, ß und o an einer Reihe wohl definierter
Plagioklase durch außerordentlich zahlreiche Messungen sorgfäl-
tig festgelegt sind, kann man zunächst y aus AIP und c nach den
auf S. 8 mitgeteilten Formeln berechnen und alsdann auch die
beiden andern Pinakoidwinkel Pk und kM, sowie den dritten
Achsenwinkel ot durch Rechnung finden. Um hier nicht nur an die
auf S. 8 verzeichneten Anorthitgehalte gebunden zu sein, sind
die ersten drei Winkel in zwei von den sechs Kurven der Figuren
5 und 6 auf Seite 20 und 21 und in der ausgezogenen Kurve der
obigen Fig. 4 graphisch dargestellt. Hier ist wie üblich der Anor-
thitgehalt in Mo].-°/(, durch die Abszissen und die Größe der
Winkel durch die Ordinaten wiedergegeben.
Der Raumersparnis wegen sind die drei Kurven für K, ß, y
in dem einen Bild, die für die Winkel AIP, Pk, kAl in dem andern
Bild vereinigt. Die Ordinaten müssen an den entsprechenden
Skalen, also
2*