Die Baeyersche Spannungstheorie und die Struktur des Diamants. (A. 7) 15
Die Vermutung lag nun sehr nahe, daß eine der anderen, oben
erwähnten Verknüpfungsarten der Cyclohexanringe (vgl. Abb. 8,
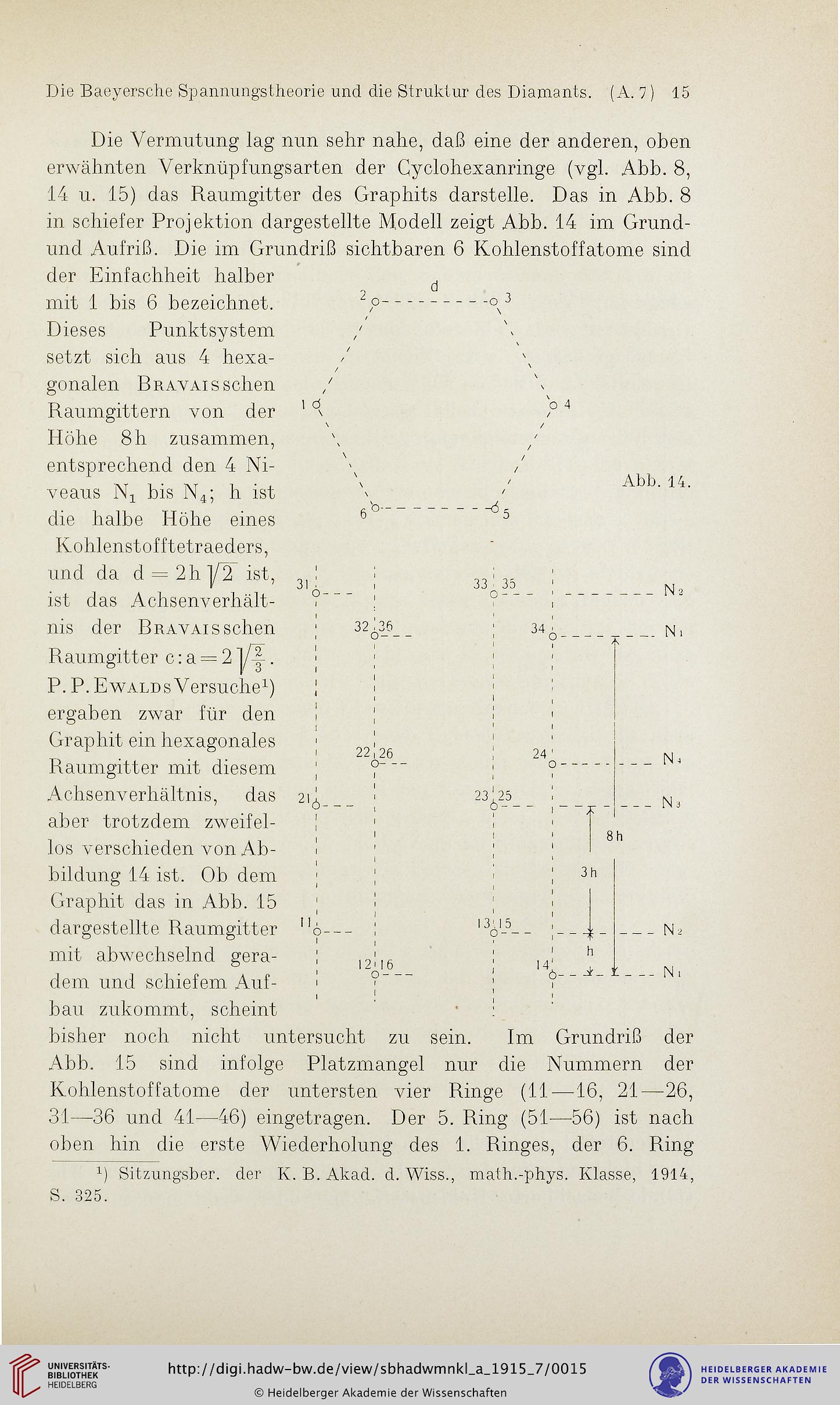
14 u. 15) das Raumgitter des Graphits darstelle. Das in Abb. 8
in schiefer Projektion dargestellte Modell zeigt Abb. 14 im Grund-
und Aufriß. Die im Grundriß sichtbaren 6 Kohlenstoffatome sind
der Einfachheit halber
d
mit 1 bis 6 bezeichnet. P-o i
Dieses Punktsystem /
setzt sich aus 4 hexa-
gonalen BRAVAis sehen
Raumgittern von der
Höhe 8 h zusammen, \ /
entsprechend den 4 Ni- - /
Abb. 14.
1 d
o 4
veaus Ni bis N^; h ist
\
'
die halbe Höhe eines
6'°- *
- ^5
Kohlenstofftetraeders,
und da d = 2h j/2 ist,
w
33 ! 33
ist das Achsenverhält-
o- -
nis der BRAVAis sehen
; 32<k6_ _
3^---
Raumgitter c: a = 2 j/V.
P. P. EwAims Versuche^)
: t
ergaben zwar für den
' ,
Graphit ein hexagonales
t
i 22^6
24 '
Raumgitter mit diesem
. o- --
! '
0-
Achsenverhältnis, das
2^25_
aber trotzdem zweifei-
<
los verschieden von Ab-
;
bildung 14 ist. Ob dem
. '
' 3h
Graphit das in Abb. 15
' !
dargestellte Raumgitter
I! .
o- ,
13'.! 5
o- -
mit abwechselnd gera-
' 1206
< h
!4' ,
dem und schiefem Auf-
' o-
6- -
bau zukommt, scheint
_N2
N.
, N-
--- N.
8h
N.
bisher noch nicht untersucht zu sein. Im Grundriß der
Abb. 15 sind infolge Platzmangel nur die Nummern der
Kohlenstoffatome der untersten vier Ringe (11—16, 21—26,
31—36 und 41—46) eingetragen. Der 5. Ring (51—56) ist nach
oben hin die erste Wiederholung des 1. Ringes, der 6. Ring
i) Sitzungsber. der K. B.Akad. d. Wiss., math.-phys. Klasse, 1914,
S. 325.
Die Vermutung lag nun sehr nahe, daß eine der anderen, oben
erwähnten Verknüpfungsarten der Cyclohexanringe (vgl. Abb. 8,
14 u. 15) das Raumgitter des Graphits darstelle. Das in Abb. 8
in schiefer Projektion dargestellte Modell zeigt Abb. 14 im Grund-
und Aufriß. Die im Grundriß sichtbaren 6 Kohlenstoffatome sind
der Einfachheit halber
d
mit 1 bis 6 bezeichnet. P-o i
Dieses Punktsystem /
setzt sich aus 4 hexa-
gonalen BRAVAis sehen
Raumgittern von der
Höhe 8 h zusammen, \ /
entsprechend den 4 Ni- - /
Abb. 14.
1 d
o 4
veaus Ni bis N^; h ist
\
'
die halbe Höhe eines
6'°- *
- ^5
Kohlenstofftetraeders,
und da d = 2h j/2 ist,
w
33 ! 33
ist das Achsenverhält-
o- -
nis der BRAVAis sehen
; 32<k6_ _
3^---
Raumgitter c: a = 2 j/V.
P. P. EwAims Versuche^)
: t
ergaben zwar für den
' ,
Graphit ein hexagonales
t
i 22^6
24 '
Raumgitter mit diesem
. o- --
! '
0-
Achsenverhältnis, das
2^25_
aber trotzdem zweifei-
<
los verschieden von Ab-
;
bildung 14 ist. Ob dem
. '
' 3h
Graphit das in Abb. 15
' !
dargestellte Raumgitter
I! .
o- ,
13'.! 5
o- -
mit abwechselnd gera-
' 1206
< h
!4' ,
dem und schiefem Auf-
' o-
6- -
bau zukommt, scheint
_N2
N.
, N-
--- N.
8h
N.
bisher noch nicht untersucht zu sein. Im Grundriß der
Abb. 15 sind infolge Platzmangel nur die Nummern der
Kohlenstoffatome der untersten vier Ringe (11—16, 21—26,
31—36 und 41—46) eingetragen. Der 5. Ring (51—56) ist nach
oben hin die erste Wiederholung des 1. Ringes, der 6. Ring
i) Sitzungsber. der K. B.Akad. d. Wiss., math.-phys. Klasse, 1914,
S. 325.