36 (A. 15)
PAUL STACHEL:
zugeordnet sind; dabei sind nur die der Reihe 5, 7, ..., angehö-
renden Primteder zu berücksichtigen.
Auch bei den Zwilhngsdarstellungen ist die Form der Multi-
plikatoren von der Stufenzahl r unabhängig. Wohl aber entschei-
det die Stufenzahl, Avelche Multiplikatoren in die Schwankungs-
funktion aufzunehmen sind. Bei genügend hoher Stufe werden
schließlich sämtliche ungeraden Primteiler der Zahlen 677^—2,
6%i + 2 von 5 ab wirksam, und es gehört zur Zahl eine
Schwankungsfunktion S^(67?,J, die für alle folgenden Stufen gültig
bleibt. Man gelangt um so später zur Funktion 6*^(6?^), je größer
die Primteiler der Zahlen 6r^—2, 677^ 6%i + 2 sind, am spätesten
also, wenn eine der Zahlen —f, 3 7^ + 1 eine Primzahl ist.
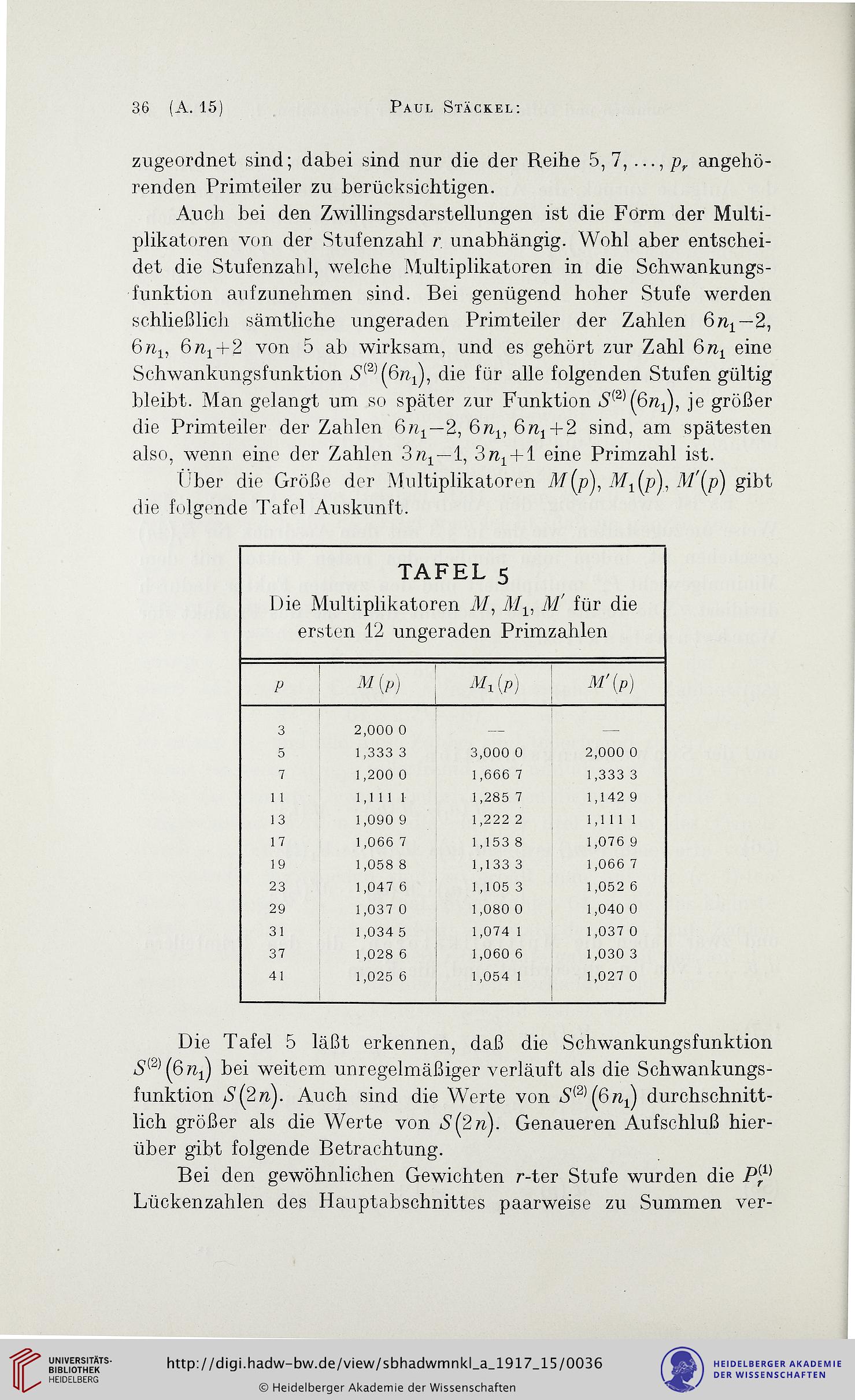
Über die Größe der Multiplikatoren 37(p), 37i(p), 3T(p) gibt
die folgende Tafel Auskunft.
TAFEL 5
Die Multiplikatoren 37, 37^, 37' für die
ersten 12 ungeraden Primzahlen
P
3
2,000 0
5
1,333 3
3,000 0
2,000 0
7
1,200 0
1,666 7
1,333 3
11
1,111 1
1,285 7
1,142 9
13
1,090 9
1,222 2
1,111 1
17
1,066 7
1,153 8
1,076 9
19
1,058 8
1,133 3
1,066 7
23
1.047 6
1,105 3
1,052 6
29
1,037 0
1,080 0
1,040 0
31
1,034 5
1,074 1
1,037 0
37
1,028 6
1,060 6
1,030 3
41
1,025 6
1,054 1
1,027 0
Die Tafel 5 läßt erkennen, daß die Schwankungsfunktion
bei weitem unregelmäßiger verläuft als die Schwankungs-
funktion 6*(2??.). Auch sind die Werte von 6^(6771) durchschnitt-
lich größer als die Werte von 6*(2 77). Genaueren Aufschluß hier-
über gibt folgende Betrachtung.
Bei den gewöhnlichen Gewichten 7*-ter Stufe wurden die
Lückenzahlen des Hauptabschnittes paarweise zu Summen ver-
PAUL STACHEL:
zugeordnet sind; dabei sind nur die der Reihe 5, 7, ..., angehö-
renden Primteder zu berücksichtigen.
Auch bei den Zwilhngsdarstellungen ist die Form der Multi-
plikatoren von der Stufenzahl r unabhängig. Wohl aber entschei-
det die Stufenzahl, Avelche Multiplikatoren in die Schwankungs-
funktion aufzunehmen sind. Bei genügend hoher Stufe werden
schließlich sämtliche ungeraden Primteiler der Zahlen 677^—2,
6%i + 2 von 5 ab wirksam, und es gehört zur Zahl eine
Schwankungsfunktion S^(67?,J, die für alle folgenden Stufen gültig
bleibt. Man gelangt um so später zur Funktion 6*^(6?^), je größer
die Primteiler der Zahlen 6r^—2, 677^ 6%i + 2 sind, am spätesten
also, wenn eine der Zahlen —f, 3 7^ + 1 eine Primzahl ist.
Über die Größe der Multiplikatoren 37(p), 37i(p), 3T(p) gibt
die folgende Tafel Auskunft.
TAFEL 5
Die Multiplikatoren 37, 37^, 37' für die
ersten 12 ungeraden Primzahlen
P
3
2,000 0
5
1,333 3
3,000 0
2,000 0
7
1,200 0
1,666 7
1,333 3
11
1,111 1
1,285 7
1,142 9
13
1,090 9
1,222 2
1,111 1
17
1,066 7
1,153 8
1,076 9
19
1,058 8
1,133 3
1,066 7
23
1.047 6
1,105 3
1,052 6
29
1,037 0
1,080 0
1,040 0
31
1,034 5
1,074 1
1,037 0
37
1,028 6
1,060 6
1,030 3
41
1,025 6
1,054 1
1,027 0
Die Tafel 5 läßt erkennen, daß die Schwankungsfunktion
bei weitem unregelmäßiger verläuft als die Schwankungs-
funktion 6*(2??.). Auch sind die Werte von 6^(6771) durchschnitt-
lich größer als die Werte von 6*(2 77). Genaueren Aufschluß hier-
über gibt folgende Betrachtung.
Bei den gewöhnlichen Gewichten 7*-ter Stufe wurden die
Lückenzahlen des Hauptabschnittes paarweise zu Summen ver-