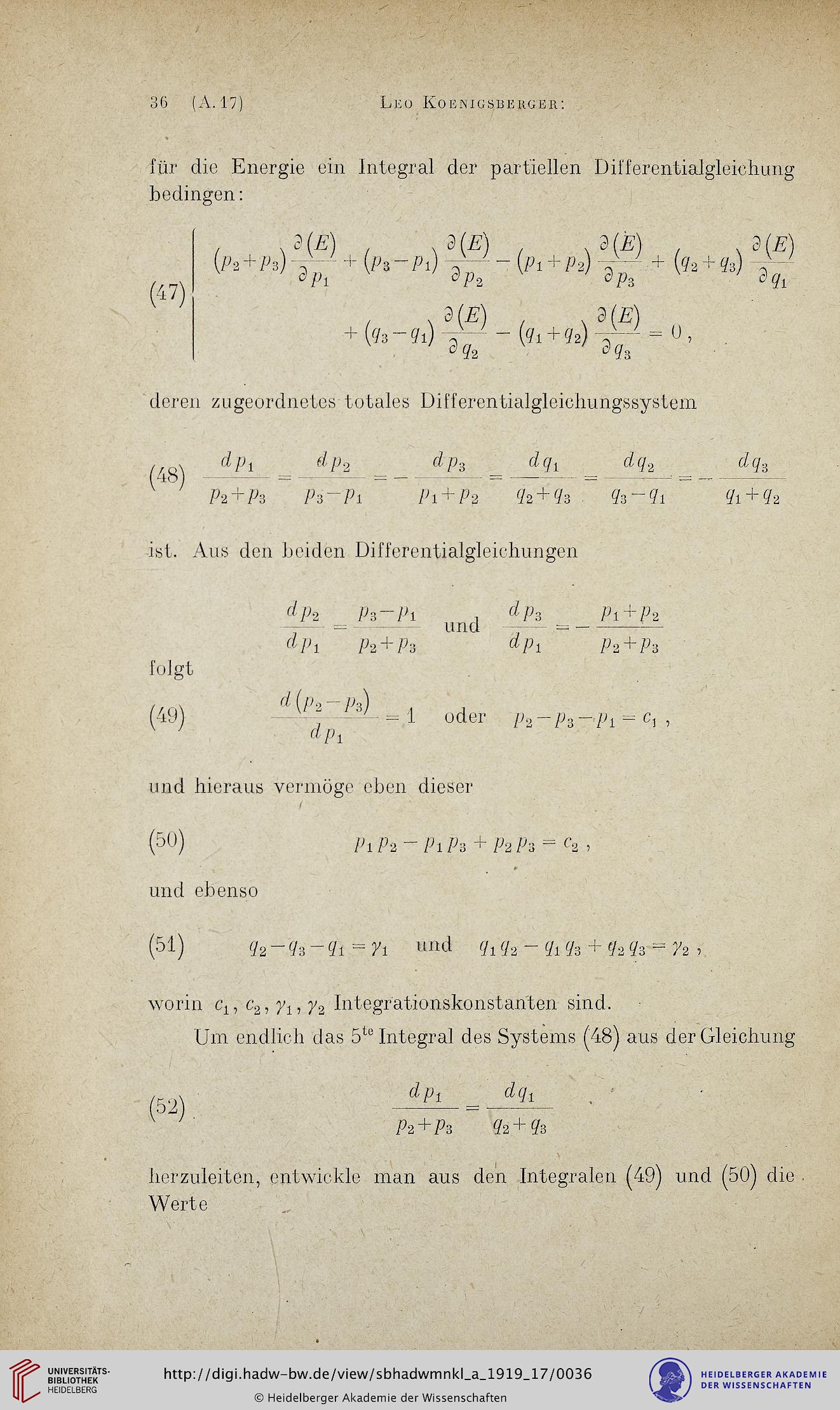DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.36507#0036
36 (A.17)
ÜEO K0E!\1CSEEHGER:
für die Energie ein integral der partiellen Differentialgleichung
bedingen:
(47)
3(7?) 3(7?) 3(7?) , .3(7?)
(Z^ + Ps) , ^ + (zG"Pi) ,, - (P1 + P2) + (72 + 73) y '
'Zh
3z+
7i
, ,37? , ,37?
+ (7s-7i) y - (71 + 72) v - = 0,
3?2 3^
deren xugeordnetes totales Differentialgleichungssystem
Z4S) ^ ^72 ^7s
Z'i Zu /E-Pi Zh + Ps 72 + 73 73-7i 7i + ?2
ist. Aus den beiden Differentialgleichungen
folgt
(49)
und hieraus vermöge eben dieser
(50) ZhP2-ZAP3 + ZAZA = c-2,
und ebenso
(51) 7s - 7s - 7i = 7i ^"0 7i 72 - 7i 7s + 72 7s = 72 1
worin Integrationskonstanten sind.
Um endlich das 5^ Integral des Systems (48) aus der Gleichung
(52) _ ^7i . * '
P2 + P3 72+73
hcrzuleitcn, entwickle man aus den Integralen (49) und (50) die
Werte
^Z4
^Pl P2+P3
und
P1+P2
Z+ + ZU
^(ZG-Ps)
dp,
i oder ZU-ZU-Zh = G,
ÜEO K0E!\1CSEEHGER:
für die Energie ein integral der partiellen Differentialgleichung
bedingen:
(47)
3(7?) 3(7?) 3(7?) , .3(7?)
(Z^ + Ps) , ^ + (zG"Pi) ,, - (P1 + P2) + (72 + 73) y '
'Zh
3z+
7i
, ,37? , ,37?
+ (7s-7i) y - (71 + 72) v - = 0,
3?2 3^
deren xugeordnetes totales Differentialgleichungssystem
Z4S) ^ ^72 ^7s
Z'i Zu /E-Pi Zh + Ps 72 + 73 73-7i 7i + ?2
ist. Aus den beiden Differentialgleichungen
folgt
(49)
und hieraus vermöge eben dieser
(50) ZhP2-ZAP3 + ZAZA = c-2,
und ebenso
(51) 7s - 7s - 7i = 7i ^"0 7i 72 - 7i 7s + 72 7s = 72 1
worin Integrationskonstanten sind.
Um endlich das 5^ Integral des Systems (48) aus der Gleichung
(52) _ ^7i . * '
P2 + P3 72+73
hcrzuleitcn, entwickle man aus den Integralen (49) und (50) die
Werte
^Z4
^Pl P2+P3
und
P1+P2
Z+ + ZU
^(ZG-Ps)
dp,
i oder ZU-ZU-Zh = G,