42
Heinz Götze
Stufe El (Abb. 21): Die Begründung für die geometrische Rich-
tigkeit der Konstruktionsstufe E wird in der Figur El gegeben, aus
der hervorgeht, daß das Quadrat AB CD ein Viertel der Fläche des
punktierten Quadrates V VI VII VIII einnimmt und damit die
Strecke a*b* gleich der Strecke Oa* ist, d. h. halb so groß wie der
Quadratdurchmesser bzw. die Quadratseiten AD oder BC. Hierauf
beruht in Stufe E die achtmalige Ansetzung eines Rechteckes an
die Seiten der Quadrate ABCD (bzw. EFGH) mit den Seitenlängen
AB
AB x -y- . Damit erhält man in fg, gh, hi und if bzw. in den ent-
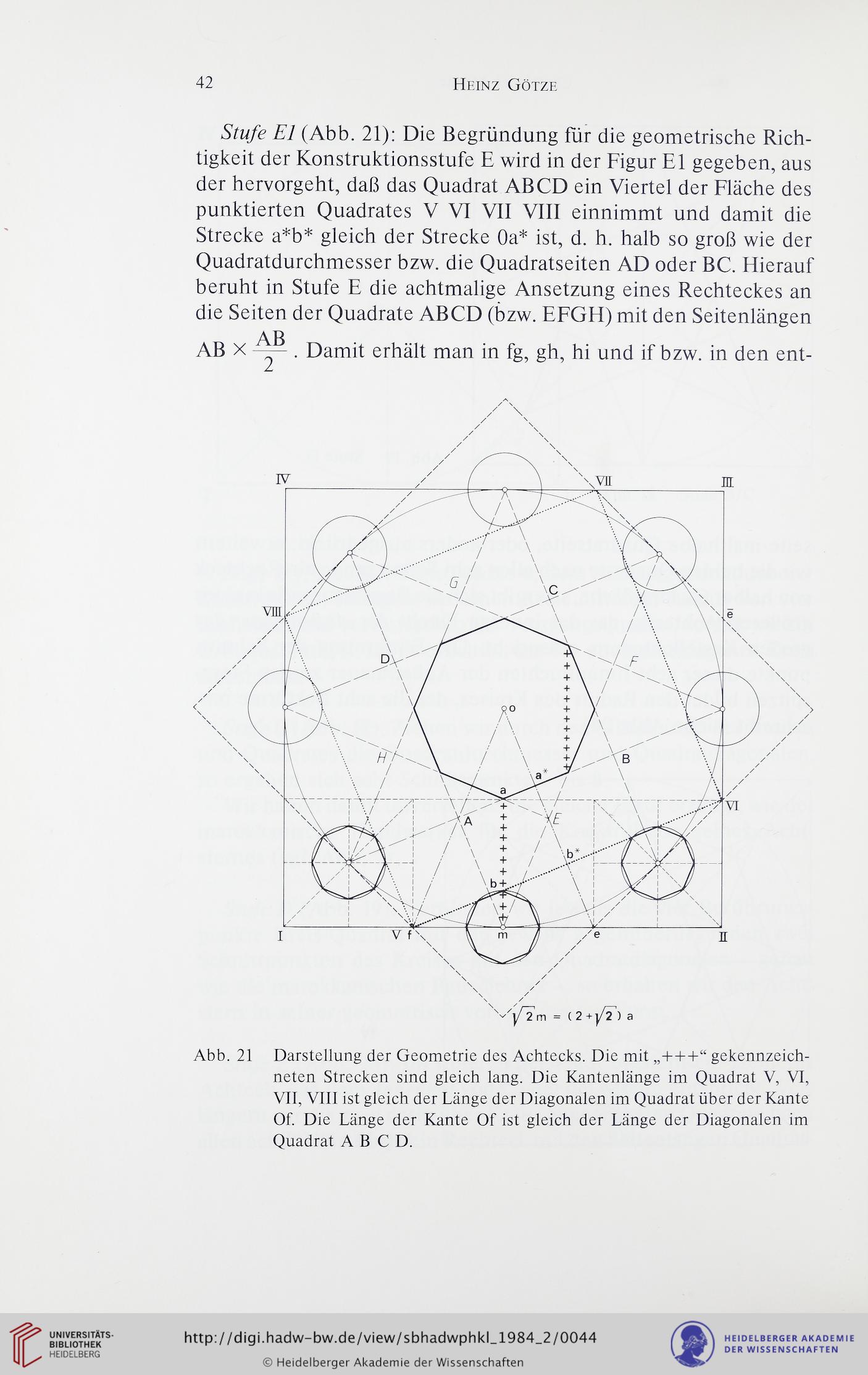
Abb. 21 Darstellung der Geometrie des Achtecks. Die mit „+++“ gekennzeich-
neten Strecken sind gleich lang. Die Kantenlänge im Quadrat V, VI,
VII, VIII ist gleich der Länge der Diagonalen im Quadrat über der Kante
Of. Die Länge der Kante Of ist gleich der Länge der Diagonalen im
Quadrat A B C D.
Heinz Götze
Stufe El (Abb. 21): Die Begründung für die geometrische Rich-
tigkeit der Konstruktionsstufe E wird in der Figur El gegeben, aus
der hervorgeht, daß das Quadrat AB CD ein Viertel der Fläche des
punktierten Quadrates V VI VII VIII einnimmt und damit die
Strecke a*b* gleich der Strecke Oa* ist, d. h. halb so groß wie der
Quadratdurchmesser bzw. die Quadratseiten AD oder BC. Hierauf
beruht in Stufe E die achtmalige Ansetzung eines Rechteckes an
die Seiten der Quadrate ABCD (bzw. EFGH) mit den Seitenlängen
AB
AB x -y- . Damit erhält man in fg, gh, hi und if bzw. in den ent-
Abb. 21 Darstellung der Geometrie des Achtecks. Die mit „+++“ gekennzeich-
neten Strecken sind gleich lang. Die Kantenlänge im Quadrat V, VI,
VII, VIII ist gleich der Länge der Diagonalen im Quadrat über der Kante
Of. Die Länge der Kante Of ist gleich der Länge der Diagonalen im
Quadrat A B C D.