Die Fundamentalkonstruktion der hyperbolischen Trigometrie.
5
Diese Lote sind die Seitenabschnitte. Es werde jeder Abschnitt dar-
gestellt durch die Seite, auf der er liegt, und den andern Abschnitt dieser
Seite. Dann gehen die Gleichungen 2 über in:
(3)
n(ZB-c) 4-77(FC-ö)=2
77(a-ZC) -n^c^ZA) = [x
- 77(& + YA)A-n(a-XB) = v
Die Gleichungen für die andern Ecken lassen sich wieder ohne Figur
hinschreiben. Die Abschnitte treten positiv auf in den Gliedern mit
negativen Vorzeichen, sie sind größer als die Seiten für den Winkel, in
dem S liegt. Also für Ecke B und C:
- n^c + ZB) +H(b-YC) = X
77 (X C — a) + 77(ZA — c) -
II (b — YA) — II (a XB} — v
n(c-ZB) -II(b+ Y C) = 2
— n (a -f- X C) + 77 (c — Z A) = ;x
n (V A — &) + n (XB — a) = v
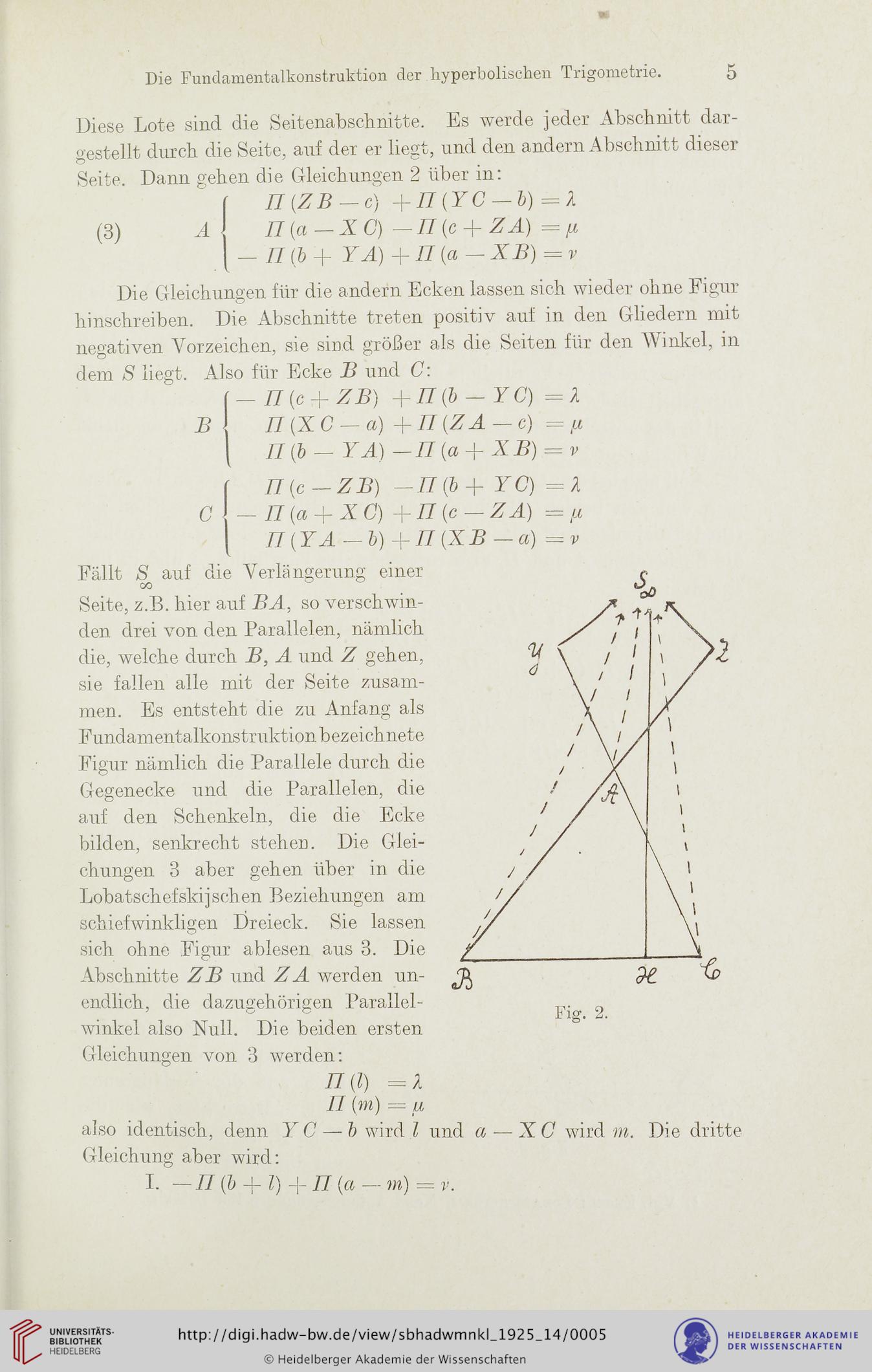
Fällt S auf die Verlängerung einer
Seite, z.B. hier auf BA, so verschwin-
den. drei von den Parallelen, nämlich
die, welche durch B, A und Z gehen,
sie fallen alle mit der Seite zusam-
men. Es entsteht die zu Anfang als
Fundamentalkonstruktionbezeichnete
Figur nämlich die Parallele durch die
Gegenecke und die Parallelen, die
auf den Schenkeln, die die Ecke
bilden, senkrecht stehen. Die Glei-
chungen 3 aber gehen über in die
Lobatsch efskij sch en Beziehungen am
schiefwinkligen Dreieck. Sie lassen
sich ohne Figur ablesen aus 3. Die
Abschnitte ZB und ZA werden un-
endlich, die dazugehörigen Parallel-
winkel also Null. Die beiden ersten
Gleichungen von 3 werden:
77(0 =7
77 (m) — ix
also identisch, denn Y C — b wird l
Gleichung aber wird:
und a — XC wird m. Die dritte
I- — 77 (& -(- 0 + 77 (a — m) -
5
Diese Lote sind die Seitenabschnitte. Es werde jeder Abschnitt dar-
gestellt durch die Seite, auf der er liegt, und den andern Abschnitt dieser
Seite. Dann gehen die Gleichungen 2 über in:
(3)
n(ZB-c) 4-77(FC-ö)=2
77(a-ZC) -n^c^ZA) = [x
- 77(& + YA)A-n(a-XB) = v
Die Gleichungen für die andern Ecken lassen sich wieder ohne Figur
hinschreiben. Die Abschnitte treten positiv auf in den Gliedern mit
negativen Vorzeichen, sie sind größer als die Seiten für den Winkel, in
dem S liegt. Also für Ecke B und C:
- n^c + ZB) +H(b-YC) = X
77 (X C — a) + 77(ZA — c) -
II (b — YA) — II (a XB} — v
n(c-ZB) -II(b+ Y C) = 2
— n (a -f- X C) + 77 (c — Z A) = ;x
n (V A — &) + n (XB — a) = v
Fällt S auf die Verlängerung einer
Seite, z.B. hier auf BA, so verschwin-
den. drei von den Parallelen, nämlich
die, welche durch B, A und Z gehen,
sie fallen alle mit der Seite zusam-
men. Es entsteht die zu Anfang als
Fundamentalkonstruktionbezeichnete
Figur nämlich die Parallele durch die
Gegenecke und die Parallelen, die
auf den Schenkeln, die die Ecke
bilden, senkrecht stehen. Die Glei-
chungen 3 aber gehen über in die
Lobatsch efskij sch en Beziehungen am
schiefwinkligen Dreieck. Sie lassen
sich ohne Figur ablesen aus 3. Die
Abschnitte ZB und ZA werden un-
endlich, die dazugehörigen Parallel-
winkel also Null. Die beiden ersten
Gleichungen von 3 werden:
77(0 =7
77 (m) — ix
also identisch, denn Y C — b wird l
Gleichung aber wird:
und a — XC wird m. Die dritte
I- — 77 (& -(- 0 + 77 (a — m) -