Die komplementären Figuren der nichteuklidischen Ebene. 5
Hypotenuse ist, die anliegenden Seiten sind gleich den Koni-
plementärstrecken der Katheten, die gegenüberliegenden
Seiten sind die Parallellote der beiden Winkel, a liegt Z
gegenüber. Zwischen den Seiten des Fünfecks bestehen die
Beziehungen der Neperschen Kegel, d. h. es ist der Kosinus
einer Seite gleich dem Produkt der Sinus der gegenüber-
liegenden und gleich dem Produkt der Kotangenten der an-
lieg e n die n S t ü c k e.
Da jede Seite des Fünfecks Hypotenuse sein kann, so ergeben
sich leicht die 5 Dreiecke
aus
Figur 2.
c
a
b l
Z/
c
l’ /t
Z? — rz
Z
b
m —
a
V
/
m
V
a y
a
m
c ? —
ß
§ 2.
Das rechtwinklige Fünfeck und die
ZU
geordneten Spitzecke
und rechtwinkligen Dreiecke.
Um außer den zugeordneten Dreiecken auch die zugeordneten
Spitzecke kennen zu lernen, sei das Fünfeck noch einer näheren Be-
trachtung unterzogen.
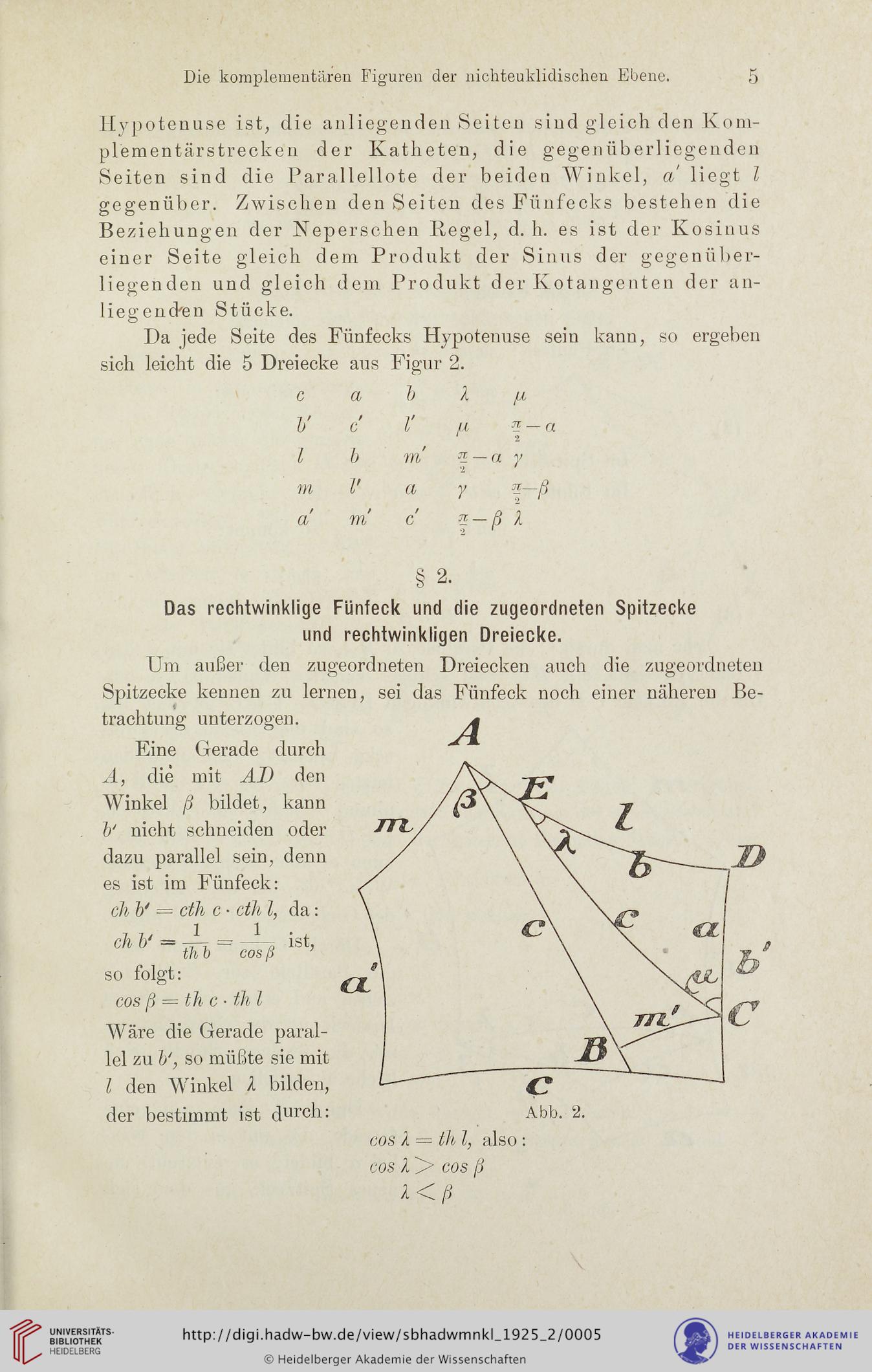
Eine Gerade durch
A, die mit Al) den
Winkel ß bildet, kann
b' nicht schneiden oder
dazu parallel sein, denn
es ist im Fünfeck:
ch &' = eth c • eth Z, da:
cfr b' — irr. — isG
th o cos ß
so folgt:
cos ß = th c • th l
Wäre die Gerade paral-
lel zu so müßte sie mit
Z den Winkel Ä bilden,
der bestimmt ist durch:
Hypotenuse ist, die anliegenden Seiten sind gleich den Koni-
plementärstrecken der Katheten, die gegenüberliegenden
Seiten sind die Parallellote der beiden Winkel, a liegt Z
gegenüber. Zwischen den Seiten des Fünfecks bestehen die
Beziehungen der Neperschen Kegel, d. h. es ist der Kosinus
einer Seite gleich dem Produkt der Sinus der gegenüber-
liegenden und gleich dem Produkt der Kotangenten der an-
lieg e n die n S t ü c k e.
Da jede Seite des Fünfecks Hypotenuse sein kann, so ergeben
sich leicht die 5 Dreiecke
aus
Figur 2.
c
a
b l
Z/
c
l’ /t
Z? — rz
Z
b
m —
a
V
/
m
V
a y
a
m
c ? —
ß
§ 2.
Das rechtwinklige Fünfeck und die
ZU
geordneten Spitzecke
und rechtwinkligen Dreiecke.
Um außer den zugeordneten Dreiecken auch die zugeordneten
Spitzecke kennen zu lernen, sei das Fünfeck noch einer näheren Be-
trachtung unterzogen.
Eine Gerade durch
A, die mit Al) den
Winkel ß bildet, kann
b' nicht schneiden oder
dazu parallel sein, denn
es ist im Fünfeck:
ch &' = eth c • eth Z, da:
cfr b' — irr. — isG
th o cos ß
so folgt:
cos ß = th c • th l
Wäre die Gerade paral-
lel zu so müßte sie mit
Z den Winkel Ä bilden,
der bestimmt ist durch: