6
Ernst Roeser :
t
Somit hat die Gerade mit b' eine gemeinsame Senkrechte. Es
entsteht das Spitzeck A B CD. Hierin ist:
(1)
(2)
(3)
cos ß = th l ■ th A B. Im Fünfeck:
C,‘ b' = (W = Aß = llä ■ Ac’ also ist:
AB — c
1 m Spitzeck: cot ß = sh A B ■ th B C
= sh c • th B C
Im Fünfeck: ch m = sh c ■ shB— S,~ oder:
shb
cot ß = = sh c- th mr, also:
' shm
B C — mf
Im Spitzeck: cos ß = sh m' sh CD
Im Fünfeck: ch B = sh a' sh m- da:
ch B — = —-a so kommt:
thb cosß
1 _ 1_
cosß sh a
CD = a
_1
sh m ’
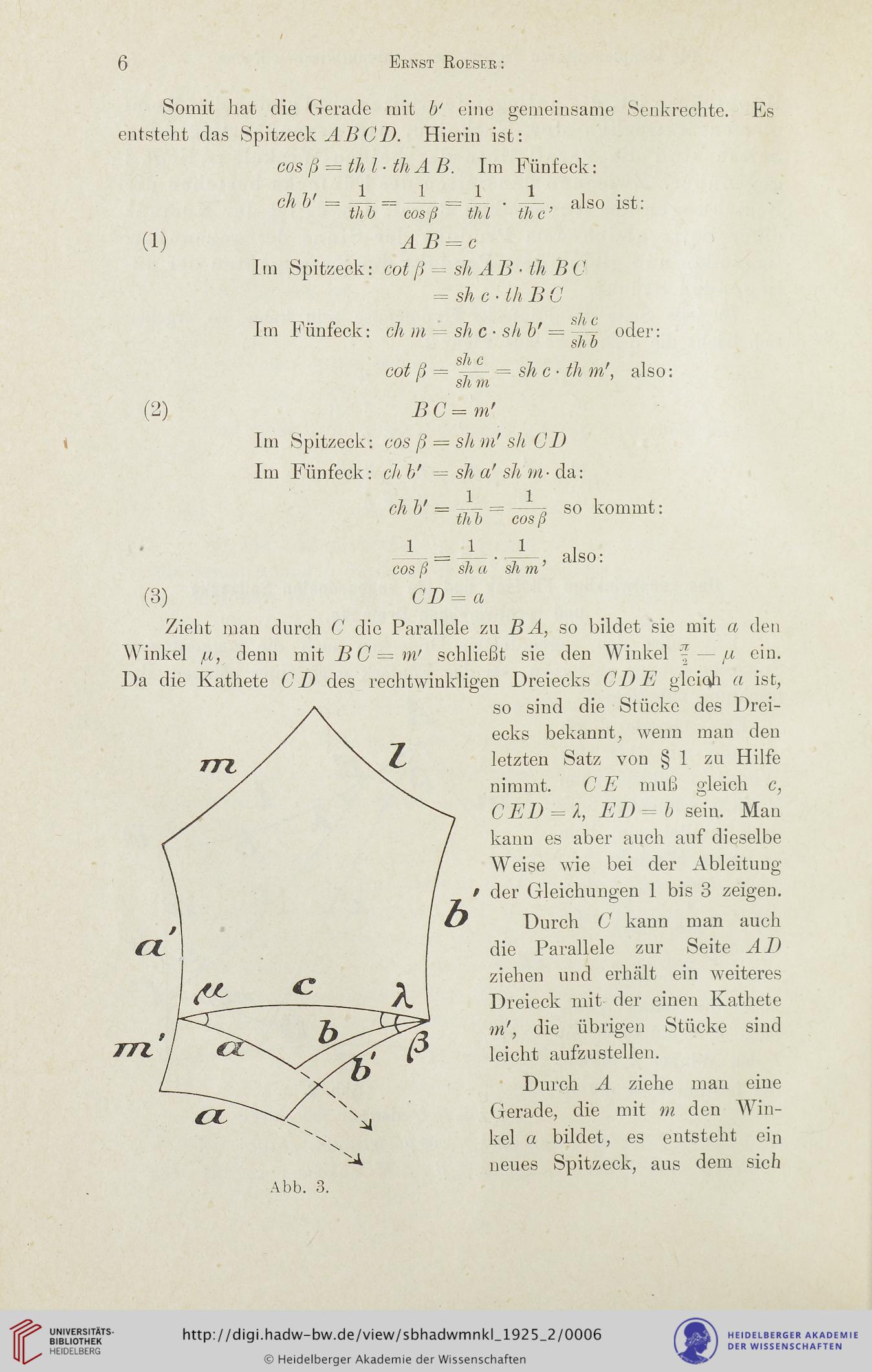
Zieht man durch C die Parallele zu B A, so bildet sie mit a den
Winkel /z, denn mit B C = m' schließt sie den Winkel I— /z ein.
Da die Kathete CD des rechtwinkligen Dreiecks CDE glciqh a ist,
so sind die Stücke des Drei-
ecks bekannt, wenn man den
letzten Satz von § 1 zu Hilfe
nimmt. C E muß gleich c,
CED — 2, ED = b sein. Man
kann es aber auch auf dieselbe
Weise wie bei der Ableitung
f der Gleichungen 1 bis 3 zeigen.
Durch C kann man auch
die Parallele zur Seite AD
ziehen und erhält ein weiteres
Dreieck mit der einen Kathete
m', die übrigen Stücke sind
leicht aufzustellen.
Durch A ziehe man eine
Gerade, die mit m den Win-
kel a bildet, es entsteht ein
neues Spitzeck, aus dem sich
Abb. 3.
Ernst Roeser :
t
Somit hat die Gerade mit b' eine gemeinsame Senkrechte. Es
entsteht das Spitzeck A B CD. Hierin ist:
(1)
(2)
(3)
cos ß = th l ■ th A B. Im Fünfeck:
C,‘ b' = (W = Aß = llä ■ Ac’ also ist:
AB — c
1 m Spitzeck: cot ß = sh A B ■ th B C
= sh c • th B C
Im Fünfeck: ch m = sh c ■ shB— S,~ oder:
shb
cot ß = = sh c- th mr, also:
' shm
B C — mf
Im Spitzeck: cos ß = sh m' sh CD
Im Fünfeck: ch B = sh a' sh m- da:
ch B — = —-a so kommt:
thb cosß
1 _ 1_
cosß sh a
CD = a
_1
sh m ’
Zieht man durch C die Parallele zu B A, so bildet sie mit a den
Winkel /z, denn mit B C = m' schließt sie den Winkel I— /z ein.
Da die Kathete CD des rechtwinkligen Dreiecks CDE glciqh a ist,
so sind die Stücke des Drei-
ecks bekannt, wenn man den
letzten Satz von § 1 zu Hilfe
nimmt. C E muß gleich c,
CED — 2, ED = b sein. Man
kann es aber auch auf dieselbe
Weise wie bei der Ableitung
f der Gleichungen 1 bis 3 zeigen.
Durch C kann man auch
die Parallele zur Seite AD
ziehen und erhält ein weiteres
Dreieck mit der einen Kathete
m', die übrigen Stücke sind
leicht aufzustellen.
Durch A ziehe man eine
Gerade, die mit m den Win-
kel a bildet, es entsteht ein
neues Spitzeck, aus dem sich
Abb. 3.