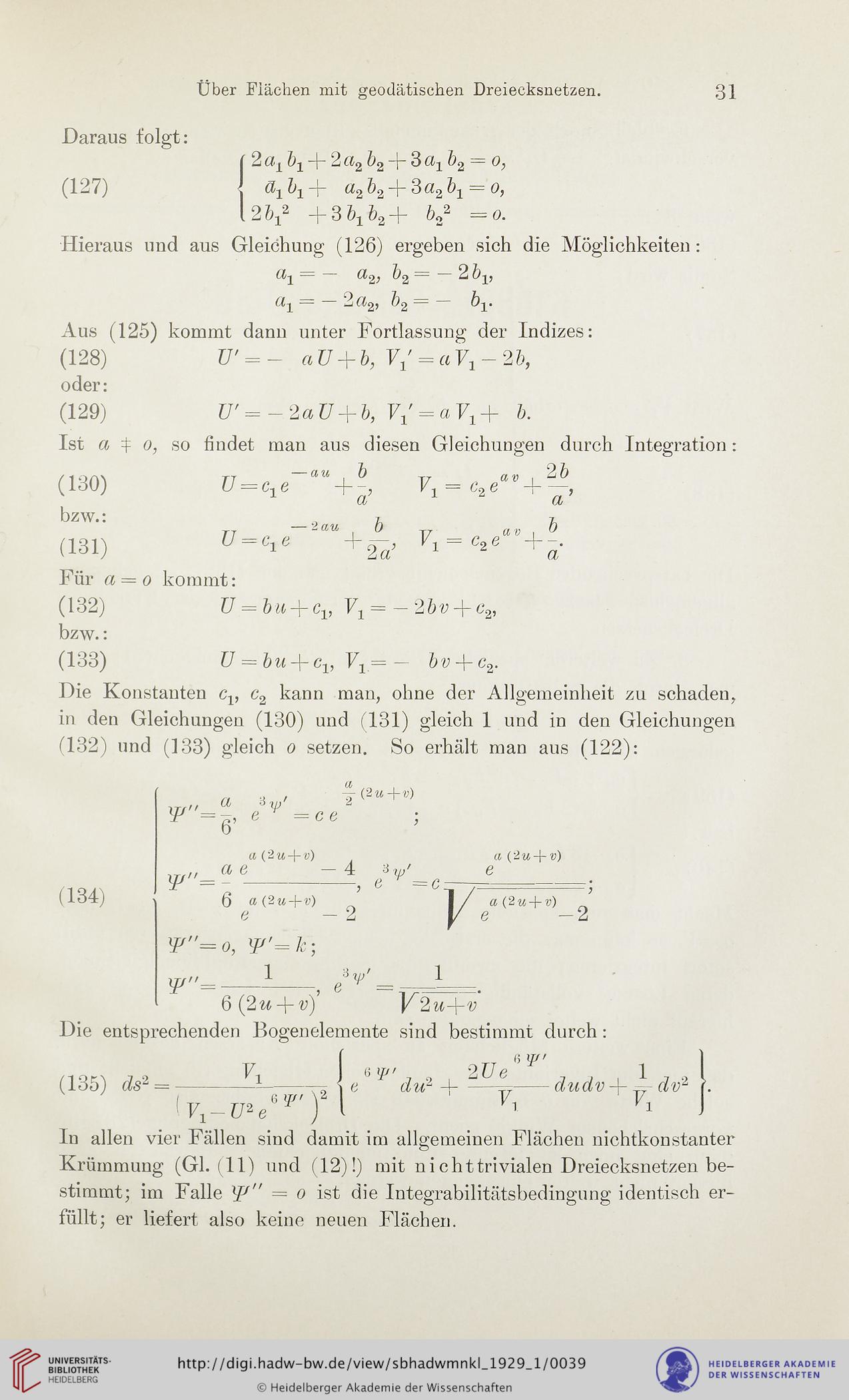Sitzungsberichte der
Heidelberger Akademie der Wissenschaften

Über Flächen mit geodätischen Dreiecksnetzen.

31

Daraus folgt:
(127)

2 tty b^ —j— 2 C^2 62 "I“ 3 ^2 — F
6j —f- 6^2 62 "f~ 3t?2 £ == F
2 fr/ +3 br b2 + b22 — o.

Hieraus und aus Gleichung (126) ergeben sich die Möglichkeiten:
= — a2) b2 — 2
= 2a2, b2 = by.
Aus (125) kommt dann unter Fortlassung der Indizes:
(128) U' = - aü + b, V/ = «Fj - 2b,
oder:
(129) U' = -2aU + b, b.
Ist a o, so findet man aus diesen Gleichungen durch Integration:
/1QA\ TT —au b „ ai) 26
(130) U — qe Fx—c2e
Cb (aj
(131) V~V +2a>
Für a = o kommt:
(132) U = &j( + c1, Fx = —2öv + c2,
bzw.:

(133) U = bu-\-c1, V1= — bvPc2.
Die Konstanten cv c2 kann man, ohne der Allgemeinheit zu schaden,
in den Gleichungen (130) und (131) gleich 1 und in den Gleichungen
(132) und (133) gleich o setzen. So erhält man aus (122):

(134)

a (2w + «)
e

In allen vier Fällen sind damit im allgemeinen Flächen nichtkonstanter
Krümmung (Gl. (11) und (12)!) mit nichttrivialen Dreiecksnetzen be-
stimmt; im Falle lP" = o ist die Integrabilitätsbedingung identisch er-
füllt ; er liefert also keine neuen Flächen.

a =c

p"=
6

£i__
T9 6 ’A' V

(2W+1>)

dudvyr dv2 ’.

J//<2“+”_2

p"=. 1_ e^'- 1_.
6(2z« + f)’
Die entsprechenden Bogenelemente sind bestimmt durch:
OTT 6?"
2üe

ITT" a iVJ
XP e =ce
6
« (2w + l>)
e — 4
a(2u+i>)
e —2