Neue Sätze
über sphärische und hyperbolische Fünfecke.
Einleitung.
Die folgenden Betrachtungen sollen zeigen, welche Bedeutung der
Komplex der komplementären Figuren für die ganze Ebene hat. Das
sphärische Fünfeck hat außerdem gewisse Eigenschaften, die beim
hyperbolischen noch nicht nachgewiesen sind. So spielen bei jenem
auch die Winkel eine Rolle, in der hyperbolischen Ebene handelt es
sich nur um Rechte, ferner läßt sich die sphärische Figur mit allen
Vierecken und Dreiecken in einem Linienzug beschreiben, woraus sich
schon die Zusammengehörigkeit der Figuren ergibt. Wir werden sehen,
daß etwas Ähnliches auch in der hyperbolischen Ebene vorhanden ist.
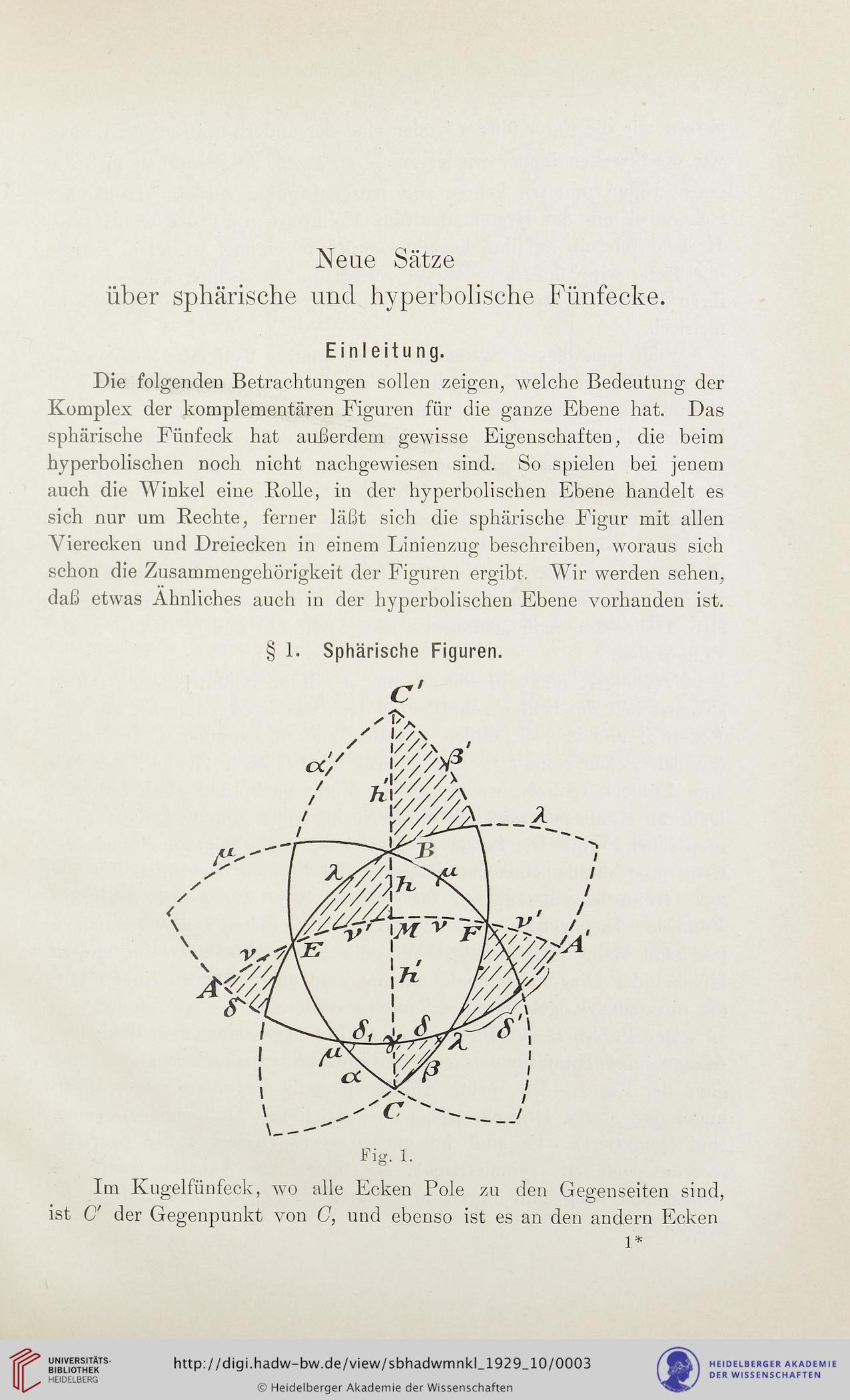
1. Sphärische Figuren.
Im Kugelfünfeck, wo alle Ecken Pole zu den Gegenseiten sind,
ist C' der Gegenpunkt von C, und ebenso ist es an den andern Ecken
1*
über sphärische und hyperbolische Fünfecke.
Einleitung.
Die folgenden Betrachtungen sollen zeigen, welche Bedeutung der
Komplex der komplementären Figuren für die ganze Ebene hat. Das
sphärische Fünfeck hat außerdem gewisse Eigenschaften, die beim
hyperbolischen noch nicht nachgewiesen sind. So spielen bei jenem
auch die Winkel eine Rolle, in der hyperbolischen Ebene handelt es
sich nur um Rechte, ferner läßt sich die sphärische Figur mit allen
Vierecken und Dreiecken in einem Linienzug beschreiben, woraus sich
schon die Zusammengehörigkeit der Figuren ergibt. Wir werden sehen,
daß etwas Ähnliches auch in der hyperbolischen Ebene vorhanden ist.
1. Sphärische Figuren.
Im Kugelfünfeck, wo alle Ecken Pole zu den Gegenseiten sind,
ist C' der Gegenpunkt von C, und ebenso ist es an den andern Ecken
1*