Über das reguläre vierdimensionale Fünfzell.
11
gelegt werden soll, ist zu beachten, daß solche Punkte nicht alle
auf einem Grenztetraeder liegen dürfen, da diese Tetraeder bereits
Projektionen des vierdimensionalen Fünfzells sind. Die Ebene
durch vier Halbierungspunkte eines solchen Tetraeders ergibt ein
ebenes Quadrat als Schnittfigur und keinen Schnittkörper. Diese
Ebene geht nicht mehr durch das vierdimensionale Fünfzell selbst.
Die erste Art von Mittelschnitten durch das Fünfzell ergibt
sich, wenn vier Punkte gewählt werden, die auf Kanten mit gemein-
samem Eckpunkt liegen. Wegen des Vorhandenseins von fünf
Eckpunkten gibt es fünf derartige ebene Schnitte, und zwar folgende
Kombinationen:
1.
I
II
III
IV: gemeinsamer Eckpunkt der zugehörigen
Kanten ist A;
2.
I
V
VI
VII: gemeinsamer Eckpunkt der zugehörigen
Kanten ist B;
3.
II
V
VIII
IX: gemeinsamer Eckpunkt der zugehörigen
Kanten ist C:
4.
III
VI
VIII
X: gemeinsamer Eckpunkt der zugehörigen
Kanten ist D;
5.
IV
VII
IX
X: gemeinsamer Eckpunkt der zugehörigen
Kanten ist E.
Von den vier Punkten dieser Systeme
zu einem regulären Dreieck, wie
auch die Fig. 3 a, b, c, d, e zeigen.
Die ,,ebenen“ Schnittkörper, die
sich aus den zugehörigen vier
Punkten ergeben, sind demnach
reguläre Tetraeder. In der Pro-
jektion auf ein Grenztetraeder
des Herdimensionalen Fünfzells
lassen sich diese Schnitte aber
natürlich auch nur als Projektion
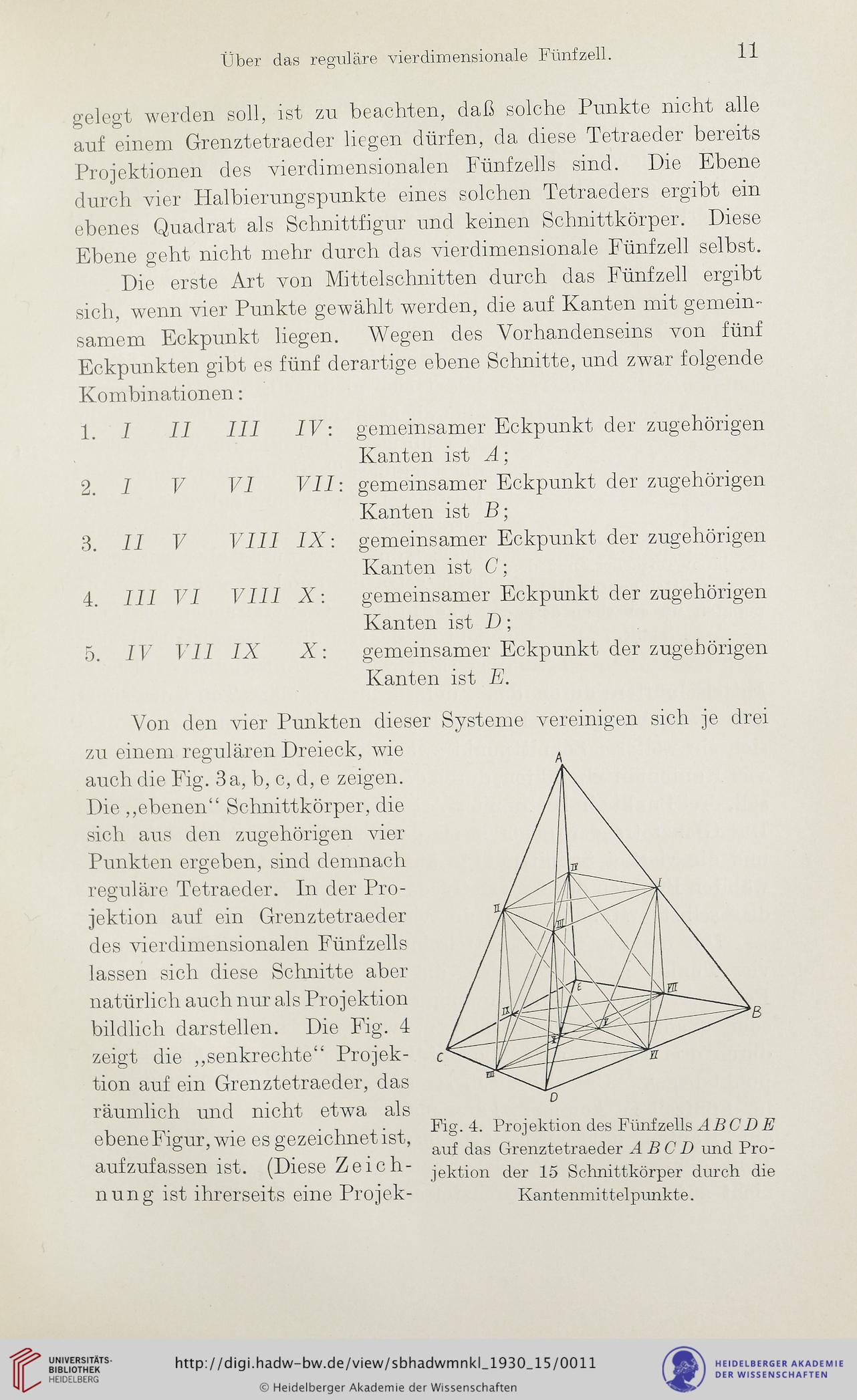
bildlich darstellen. Die Fig. 4
zeigt die „senkrechte“ Projek-
tion auf ein Grenztetraeder, das
räumlich und nicht etwa als
ebene Figur, wie es gezeichnet ist,
aufzufassen ist. (Diese Zeich-
nung ist ihrerseits eine Projek-
vereinigen sich je drei
Fig. 4. Projektion des Fünfzells ABCD E
auf das Grenztetraeder A B C D und Pro-
jektion der 15 Schnittkörper durch die
Kantenmittelpunkte.
11
gelegt werden soll, ist zu beachten, daß solche Punkte nicht alle
auf einem Grenztetraeder liegen dürfen, da diese Tetraeder bereits
Projektionen des vierdimensionalen Fünfzells sind. Die Ebene
durch vier Halbierungspunkte eines solchen Tetraeders ergibt ein
ebenes Quadrat als Schnittfigur und keinen Schnittkörper. Diese
Ebene geht nicht mehr durch das vierdimensionale Fünfzell selbst.
Die erste Art von Mittelschnitten durch das Fünfzell ergibt
sich, wenn vier Punkte gewählt werden, die auf Kanten mit gemein-
samem Eckpunkt liegen. Wegen des Vorhandenseins von fünf
Eckpunkten gibt es fünf derartige ebene Schnitte, und zwar folgende
Kombinationen:
1.
I
II
III
IV: gemeinsamer Eckpunkt der zugehörigen
Kanten ist A;
2.
I
V
VI
VII: gemeinsamer Eckpunkt der zugehörigen
Kanten ist B;
3.
II
V
VIII
IX: gemeinsamer Eckpunkt der zugehörigen
Kanten ist C:
4.
III
VI
VIII
X: gemeinsamer Eckpunkt der zugehörigen
Kanten ist D;
5.
IV
VII
IX
X: gemeinsamer Eckpunkt der zugehörigen
Kanten ist E.
Von den vier Punkten dieser Systeme
zu einem regulären Dreieck, wie
auch die Fig. 3 a, b, c, d, e zeigen.
Die ,,ebenen“ Schnittkörper, die
sich aus den zugehörigen vier
Punkten ergeben, sind demnach
reguläre Tetraeder. In der Pro-
jektion auf ein Grenztetraeder
des Herdimensionalen Fünfzells
lassen sich diese Schnitte aber
natürlich auch nur als Projektion
bildlich darstellen. Die Fig. 4
zeigt die „senkrechte“ Projek-
tion auf ein Grenztetraeder, das
räumlich und nicht etwa als
ebene Figur, wie es gezeichnet ist,
aufzufassen ist. (Diese Zeich-
nung ist ihrerseits eine Projek-
vereinigen sich je drei
Fig. 4. Projektion des Fünfzells ABCD E
auf das Grenztetraeder A B C D und Pro-
jektion der 15 Schnittkörper durch die
Kantenmittelpunkte.