DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.43614#0018
18
Ernst Jänecke:
natürlich zu berücksichtigen ist, daß diese nur das eine Grenz-
tetraeder richtig wiedergibt, die Schnittkörper aber als Projek-
tionen auf dasselbe. Dadurch erscheinen die Schnittkörper ver-
zerrt und nicht in ihrer richtigen Größe. Für die Konstruktion
beliebiger Schnitte ist aber die Fig. 4 besonders geeignet, wobei
die zunächst erhaltenen Körper nachher bei Benutzung der in den
Fig. 3a, b, c, d, e dargestellten Körper unschwer in die Körper
mit richtigen Abmessungen überführt werden können.
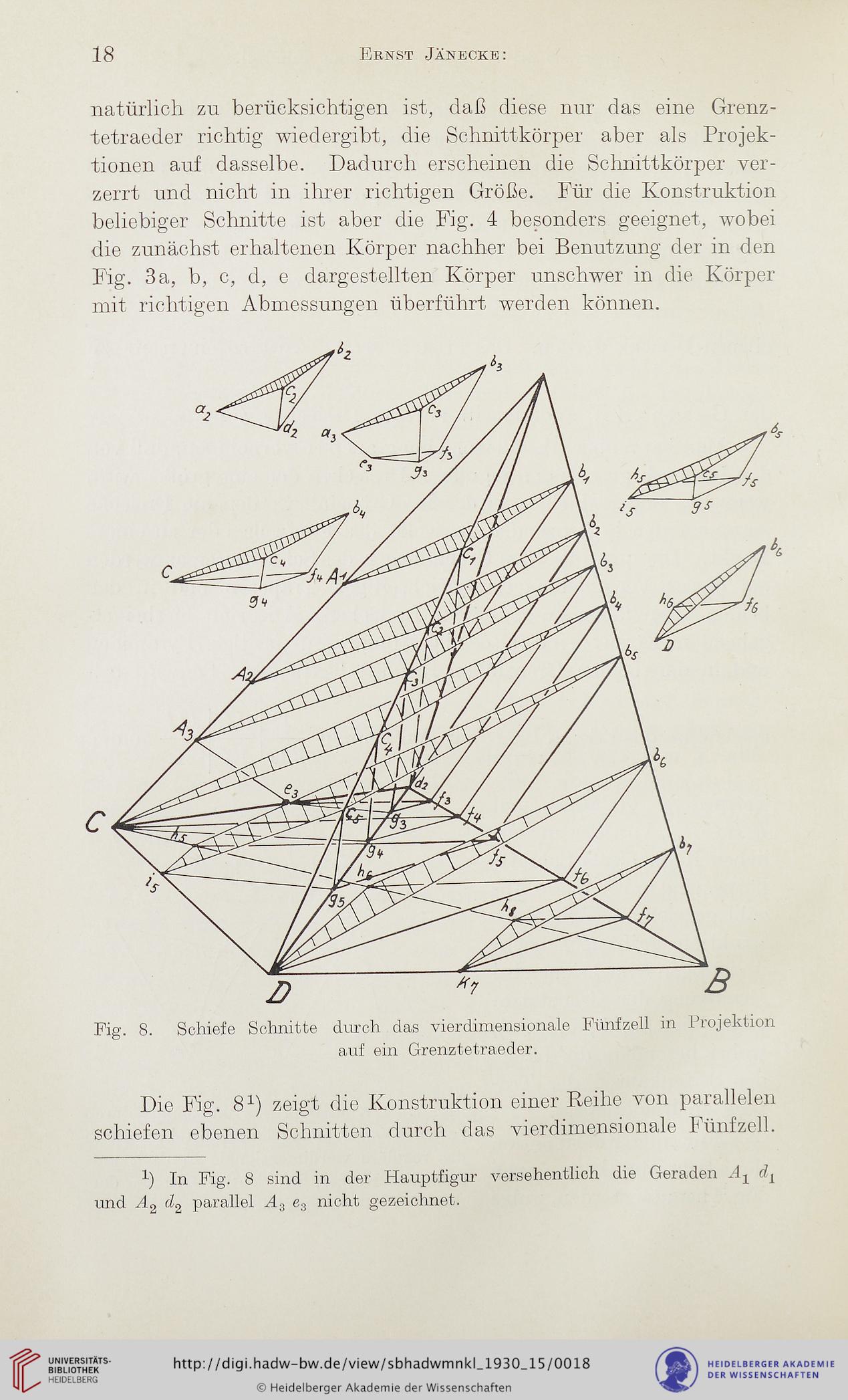
Fig. 8. Schiefe Schnitte durch das vierdimensionale Fünfzell in Projektion
auf ein Grenztetraeder.
Die Fig. 81) zeigt die Konstruktion einer Reihe von parallelen
schiefen ebenen Schnitten durch das vierdimensionale Fünfzell.
x) In Fig. 8 sind in der Hauptfigur versehentlich die Geraden A1
und Ä2 d2 parallel Ä3 e3 nicht gezeichnet.
Ernst Jänecke:
natürlich zu berücksichtigen ist, daß diese nur das eine Grenz-
tetraeder richtig wiedergibt, die Schnittkörper aber als Projek-
tionen auf dasselbe. Dadurch erscheinen die Schnittkörper ver-
zerrt und nicht in ihrer richtigen Größe. Für die Konstruktion
beliebiger Schnitte ist aber die Fig. 4 besonders geeignet, wobei
die zunächst erhaltenen Körper nachher bei Benutzung der in den
Fig. 3a, b, c, d, e dargestellten Körper unschwer in die Körper
mit richtigen Abmessungen überführt werden können.
Fig. 8. Schiefe Schnitte durch das vierdimensionale Fünfzell in Projektion
auf ein Grenztetraeder.
Die Fig. 81) zeigt die Konstruktion einer Reihe von parallelen
schiefen ebenen Schnitten durch das vierdimensionale Fünfzell.
x) In Fig. 8 sind in der Hauptfigur versehentlich die Geraden A1
und Ä2 d2 parallel Ä3 e3 nicht gezeichnet.