Sphärische und hyperbolische Vielecke.
§ 1.
Die folgenden Untersuchungen dienen der weiteren Klärung und
Verallgemeinerung des Problems der komplementären Figuren in
den beiden Geometrien. Was wird zunächst aus dem GAUss’schen
Pentagramm, wenn man zu höherer Seitenzahl übergeht ? Die Ver-
allgemeinerung bietet keine Schwierigkeiten, wenn man nicht die
drei-rechtwinkligen Stumpfecke als zugeordnete Figuren betrachtet,
sondern die Vierecke mit einspringenden Ecken, die sich dem
Fünfeck anschmiegen; auch sie enthalten alle fünf Stücke. Mit an-
deren Worten: komplementäre Figuren seien die, welche das innere
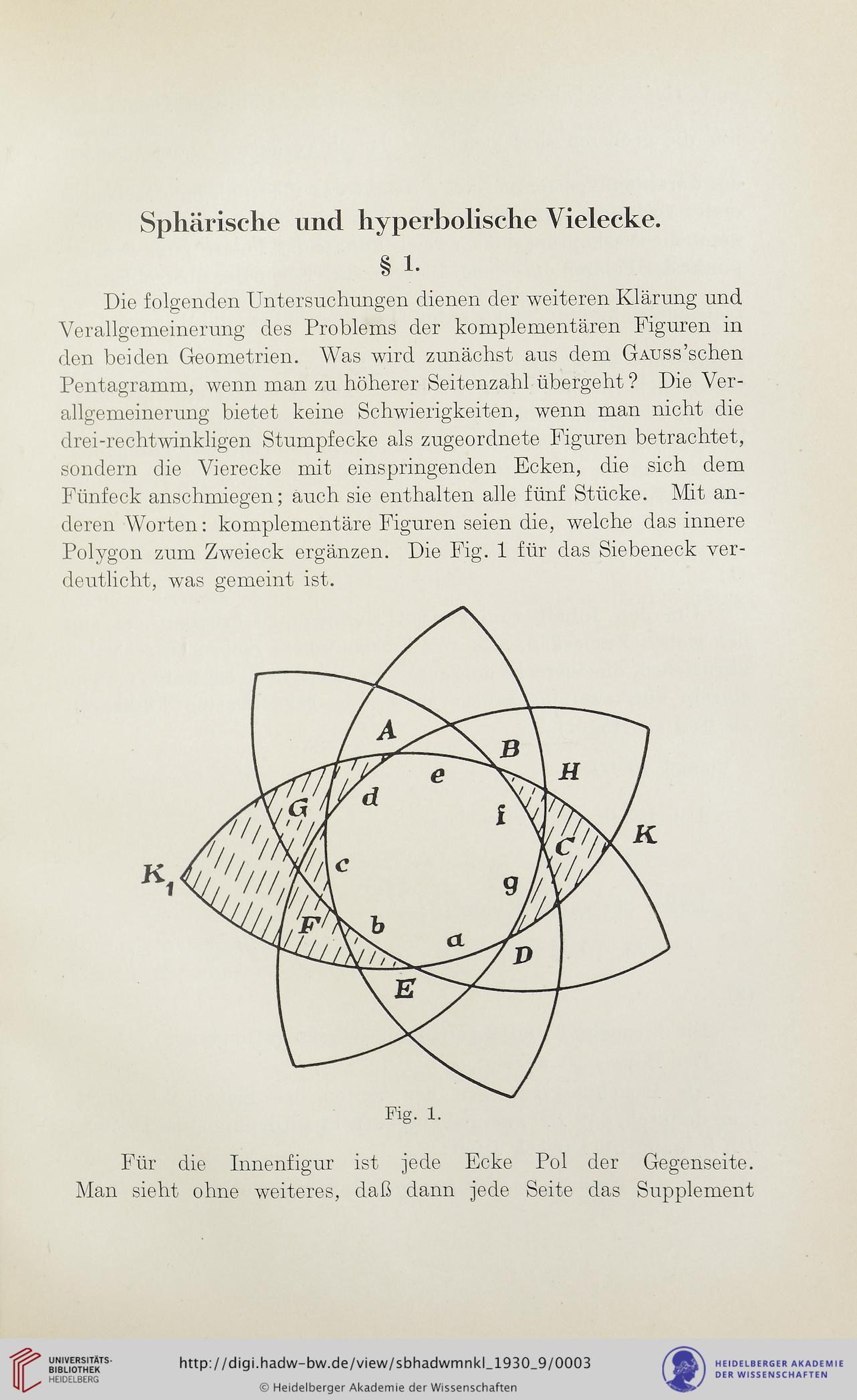
Polygon zum Zweieck ergänzen. Die Fig. 1 für das Siebeneck ver-
deutlicht, was gemeint ist.
Für die Innenfigur ist jede Ecke Pol der Gegenseite.
Man sieht ohne weiteres, daß dann jede Seite das Supplement
§ 1.
Die folgenden Untersuchungen dienen der weiteren Klärung und
Verallgemeinerung des Problems der komplementären Figuren in
den beiden Geometrien. Was wird zunächst aus dem GAUss’schen
Pentagramm, wenn man zu höherer Seitenzahl übergeht ? Die Ver-
allgemeinerung bietet keine Schwierigkeiten, wenn man nicht die
drei-rechtwinkligen Stumpfecke als zugeordnete Figuren betrachtet,
sondern die Vierecke mit einspringenden Ecken, die sich dem
Fünfeck anschmiegen; auch sie enthalten alle fünf Stücke. Mit an-
deren Worten: komplementäre Figuren seien die, welche das innere
Polygon zum Zweieck ergänzen. Die Fig. 1 für das Siebeneck ver-
deutlicht, was gemeint ist.
Für die Innenfigur ist jede Ecke Pol der Gegenseite.
Man sieht ohne weiteres, daß dann jede Seite das Supplement