Eine Schrift v.Ensheim „ Itecherches sur les calculs differentiel et integral“. (A. 7) 99
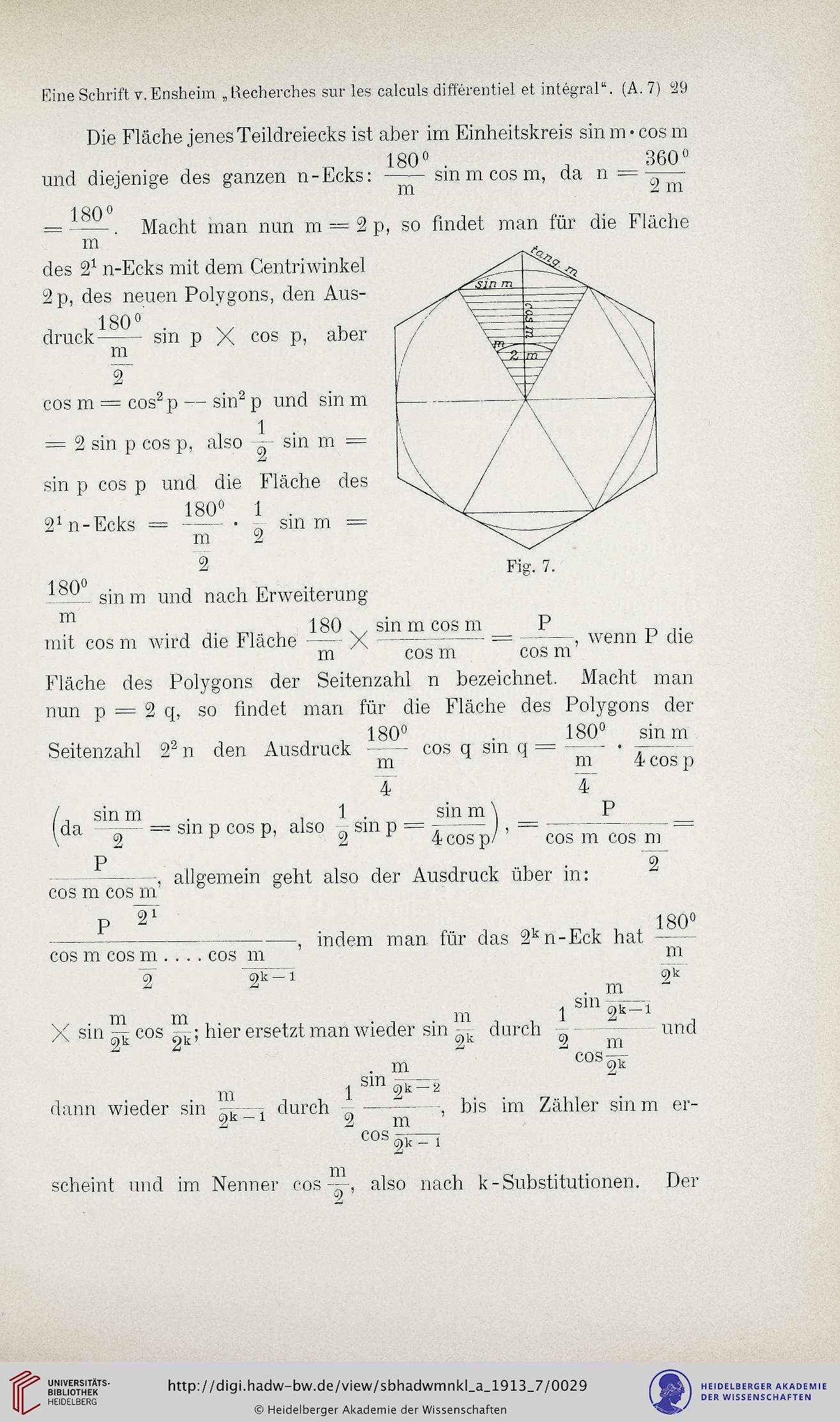
Die Fläche jenes Teilclreiecks ist aber im Einheitskreis sin m • cos m
jp i 180° . , 360°
und diejenige des ganzen n-Ecks: sinnt cos m, da n -
m
'i m
180'
. Macht man nun m — 2 p, so findet man für die Fläche
m
des 21 n-Ecks mit dem Centriwinkel
2 p, des neuen Polygons, den Aus-
180°
druck
m
2~
sin p X cos P» aber
cos m = cos2p — sin2 p und sin m
1
= 2 sin p cos p, also — sin m -
sin p cos p und die Fläche des
oi f i 180° 1 •
21 n - Ecks
180°
sm m
m
X
sin m und nach Erweiterung
m
180 sin m cos m P
mit cos m wird die 1 lache-X-• = — —, wenn P die
m cos m cos m
Fläche des Polygons der Seitenzahl n bezeichnet. Macht man
nun p = 2 q, so findet man für die Fläche des Polygons der
Seitenzahl 22n den Ausdruck —— cos q sin q — —— • S*n-Ul
m m 4 cos p
4
, sin m . 1 . sin m
da -- == sm p cos p, also — sm p -
4
2 r ~ 2 r 4cosp/’ cos m cos m
P . 2
cos m cos m
n 21
, allgemein geht also der Ausdruck über in:
cos m cos m . . . . cos m
9 ü)k — 1
, indem man für das 2kn-Eck hat
180°
m
ö)k
. m
m m m |Sinc)k-i
X sin -r cos =rr; hier ersetzt man wieder sin durch — und
2k 2k 2k 2 m
. m cos9k
lS1112k=2
dann wieder sin , durch —-. bis im Zähler sin m er-
m
9k — 1
2
cos
9k- 1
Hl
scheint und im Nenner cos -, also nach k-Substitutionen. Der
Die Fläche jenes Teilclreiecks ist aber im Einheitskreis sin m • cos m
jp i 180° . , 360°
und diejenige des ganzen n-Ecks: sinnt cos m, da n -
m
'i m
180'
. Macht man nun m — 2 p, so findet man für die Fläche
m
des 21 n-Ecks mit dem Centriwinkel
2 p, des neuen Polygons, den Aus-
180°
druck
m
2~
sin p X cos P» aber
cos m = cos2p — sin2 p und sin m
1
= 2 sin p cos p, also — sin m -
sin p cos p und die Fläche des
oi f i 180° 1 •
21 n - Ecks
180°
sm m
m
X
sin m und nach Erweiterung
m
180 sin m cos m P
mit cos m wird die 1 lache-X-• = — —, wenn P die
m cos m cos m
Fläche des Polygons der Seitenzahl n bezeichnet. Macht man
nun p = 2 q, so findet man für die Fläche des Polygons der
Seitenzahl 22n den Ausdruck —— cos q sin q — —— • S*n-Ul
m m 4 cos p
4
, sin m . 1 . sin m
da -- == sm p cos p, also — sm p -
4
2 r ~ 2 r 4cosp/’ cos m cos m
P . 2
cos m cos m
n 21
, allgemein geht also der Ausdruck über in:
cos m cos m . . . . cos m
9 ü)k — 1
, indem man für das 2kn-Eck hat
180°
m
ö)k
. m
m m m |Sinc)k-i
X sin -r cos =rr; hier ersetzt man wieder sin durch — und
2k 2k 2k 2 m
. m cos9k
lS1112k=2
dann wieder sin , durch —-. bis im Zähler sin m er-
m
9k — 1
2
cos
9k- 1
Hl
scheint und im Nenner cos -, also nach k-Substitutionen. Der