Direkte lichtelektrische Methode.
(A. 19) 21
Falls unser ganzer Gedankengang richtig ist und falls die
gefundenen Verteilungskurven fehlerfrei sind, muß einem bestimm-
ten magnetischen Felde eine bestimmte Voltgeschwindigkeit,
bzw. ein kleiner Bereich von Voltgeschwindigkeiten entsprechen,
der sich nach den geometrischen Bedingungen richtet. Diese
Voltgeschwindigkeit läßt sich unmittelbar dadurch ermitteln, daß
man bei konstantem Magnetfelde dem Käfig K variable Gegen-
spannung gibt und die Elektronenmenge bestimmt, welche eine
größere Geschwindigkeit als die angelegte Gegenspannung besitzt.
Die aus dem Magnetfeld und die aus der Voltkurve berechnete
Geschwindigkeit muß dann gleich ausfallen.
Die Kontrolle läßt sich umgekehrt auch als eine ^ Bestim-
mung auffassen. Falls es also mittels unserer Anordnung für ein
beliebiges Magnetfeld gelingt, den richtigen ^G-Wert zu erhalten,
sind alle etwaigen Bedenken beseitigt.
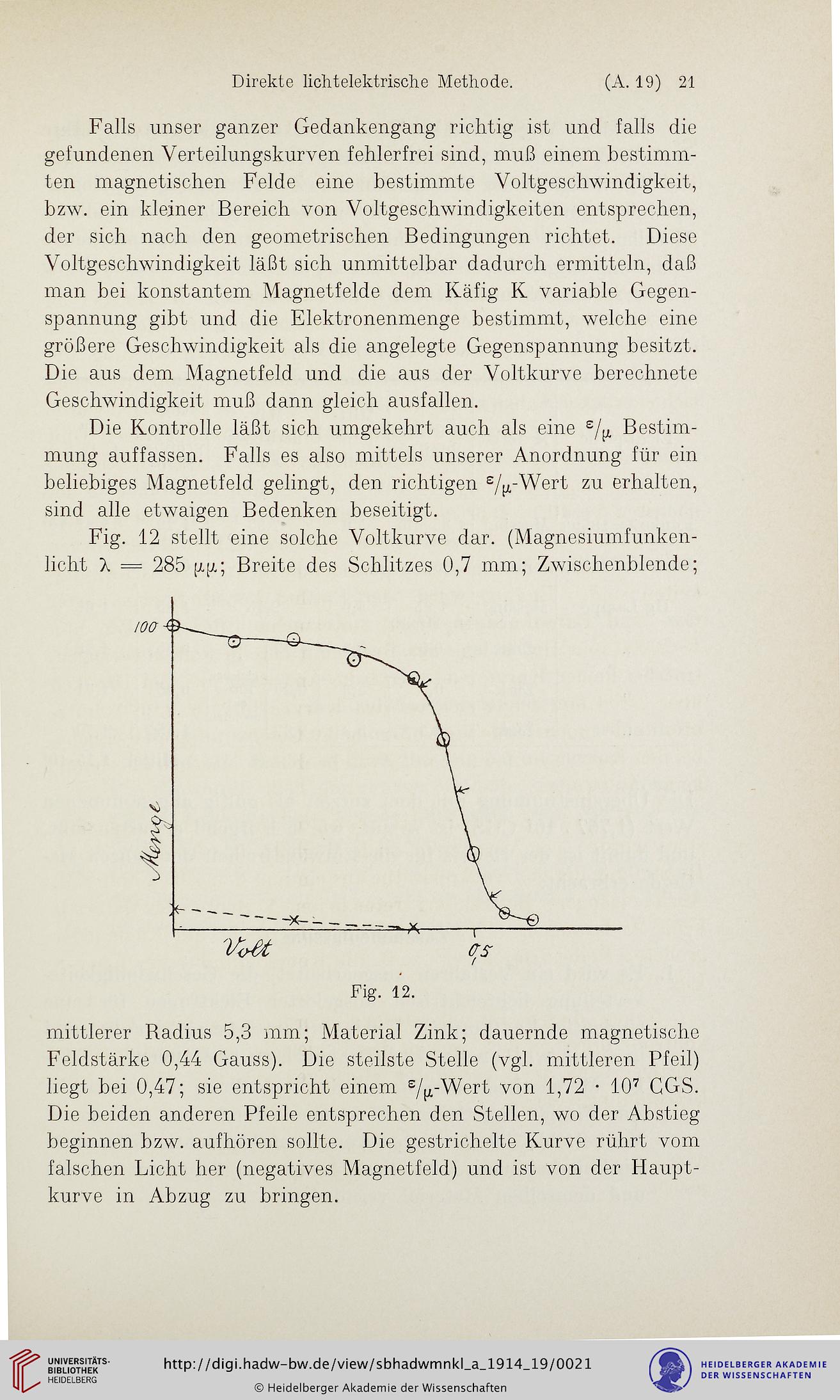
Fig. 12 stellt eine solche Voltkurve dar. (Magnesiumfunken-
licht X = 285 [jLg; Breite des Schlitzes 0,7 mm; Zwischenblende;
mittlerer Radius 5,3 mm; Material Zink; dauernde magnetische
Feldstärke 0,44 Gauss). Die steilste Stelle (vgl. mittleren Pfeil)
liegt bei 0,47; sie entspricht einem s/^-Wert von 1,72 - 10? CGS.
Die beiden anderen Pfeile entsprechen den Stellen, wo der Abstieg
beginnen bzw. aufhören sollte. Die gestrichelte Kurve rührt vom
falschen Licht her (negatives Magnetfeld) und ist von der Haupt-
kurve in Abzug zu bringen.
(A. 19) 21
Falls unser ganzer Gedankengang richtig ist und falls die
gefundenen Verteilungskurven fehlerfrei sind, muß einem bestimm-
ten magnetischen Felde eine bestimmte Voltgeschwindigkeit,
bzw. ein kleiner Bereich von Voltgeschwindigkeiten entsprechen,
der sich nach den geometrischen Bedingungen richtet. Diese
Voltgeschwindigkeit läßt sich unmittelbar dadurch ermitteln, daß
man bei konstantem Magnetfelde dem Käfig K variable Gegen-
spannung gibt und die Elektronenmenge bestimmt, welche eine
größere Geschwindigkeit als die angelegte Gegenspannung besitzt.
Die aus dem Magnetfeld und die aus der Voltkurve berechnete
Geschwindigkeit muß dann gleich ausfallen.
Die Kontrolle läßt sich umgekehrt auch als eine ^ Bestim-
mung auffassen. Falls es also mittels unserer Anordnung für ein
beliebiges Magnetfeld gelingt, den richtigen ^G-Wert zu erhalten,
sind alle etwaigen Bedenken beseitigt.
Fig. 12 stellt eine solche Voltkurve dar. (Magnesiumfunken-
licht X = 285 [jLg; Breite des Schlitzes 0,7 mm; Zwischenblende;
mittlerer Radius 5,3 mm; Material Zink; dauernde magnetische
Feldstärke 0,44 Gauss). Die steilste Stelle (vgl. mittleren Pfeil)
liegt bei 0,47; sie entspricht einem s/^-Wert von 1,72 - 10? CGS.
Die beiden anderen Pfeile entsprechen den Stellen, wo der Abstieg
beginnen bzw. aufhören sollte. Die gestrichelte Kurve rührt vom
falschen Licht her (negatives Magnetfeld) und ist von der Haupt-
kurve in Abzug zu bringen.