Beiträge zur Kritik der Differentialgeometrie. (A. 2) 11
dartun, daß die Analysis in manchen Fällen versagt: ,,Voilä donc
encore ici le calcul en defaut."
Aus der Gleichung (2) folgt die Differentialgleichung:
(4) dy = da: j/ (A—3Q 1.
Integriert man von % = 1 bis a = 0 mit dem Anfangswert ?/ = 1
und negativem Vorzeichen der Quadratwurzel, so wächst y während
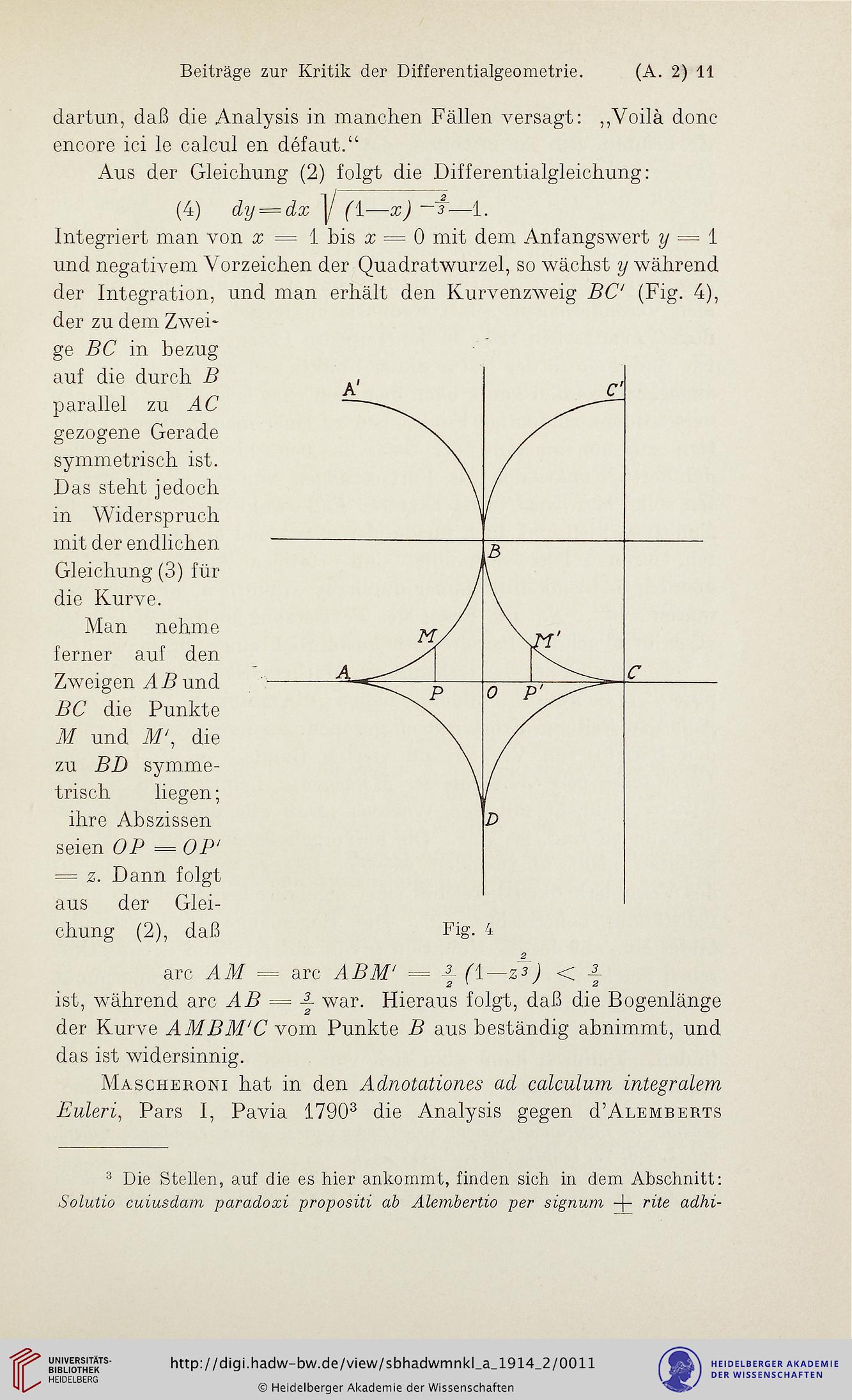
der Integration, und man erhält den Kurvenzweig PC (Fig. 4),
der zu dem Zwei*
ge PP in bezug
auf die durch P
parallel zu AP
gezogene Gerade
symmetrisch ist.
Das steht jedoch
in Widerspruch
mit der endlichen
Gleichung (3) für
die Kurve.
Man nehme
ferner auf den
Zweigen AZ? und
PP die Punkte
Af und Af, die
zu PD symme-
trisch liegen;
ihre Abszissen
seien DP = PP^
= z. Dann folgt
aus der Glei-
chung (2), daß Fig. 4
arc AAf = arc AP AP = ^ (A—z^) < ^
ist, während arc AP = ^ war. Hieraus folgt, daß die Bogenlänge
der Kurve AAfPAPP vom Punkte P aus beständig abnimmt, und
das ist widersinnig.
MASCHERONI hat in den APmüAhme.s' ad cnhn?n7% PAegrnPm
FzAeri, Pars I, Pavia 179(P die Analysis gegen d'ALEMBERTS
3 Die Stellen, auf die es hier ankommt, finden sich in dem Abschnitt:
tSo/aha caias^aw para^oaa proposih a& AA/a&erüo per sigaam -F rde acdü-
dartun, daß die Analysis in manchen Fällen versagt: ,,Voilä donc
encore ici le calcul en defaut."
Aus der Gleichung (2) folgt die Differentialgleichung:
(4) dy = da: j/ (A—3Q 1.
Integriert man von % = 1 bis a = 0 mit dem Anfangswert ?/ = 1
und negativem Vorzeichen der Quadratwurzel, so wächst y während
der Integration, und man erhält den Kurvenzweig PC (Fig. 4),
der zu dem Zwei*
ge PP in bezug
auf die durch P
parallel zu AP
gezogene Gerade
symmetrisch ist.
Das steht jedoch
in Widerspruch
mit der endlichen
Gleichung (3) für
die Kurve.
Man nehme
ferner auf den
Zweigen AZ? und
PP die Punkte
Af und Af, die
zu PD symme-
trisch liegen;
ihre Abszissen
seien DP = PP^
= z. Dann folgt
aus der Glei-
chung (2), daß Fig. 4
arc AAf = arc AP AP = ^ (A—z^) < ^
ist, während arc AP = ^ war. Hieraus folgt, daß die Bogenlänge
der Kurve AAfPAPP vom Punkte P aus beständig abnimmt, und
das ist widersinnig.
MASCHERONI hat in den APmüAhme.s' ad cnhn?n7% PAegrnPm
FzAeri, Pars I, Pavia 179(P die Analysis gegen d'ALEMBERTS
3 Die Stellen, auf die es hier ankommt, finden sich in dem Abschnitt:
tSo/aha caias^aw para^oaa proposih a& AA/a&erüo per sigaam -F rde acdü-