DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.37446#0003
1. Problemstellung.
Gegeben sei eine geschlossene RiEMANNSche Fläche T vom
Geschlechte p; auf T seien s, im Endlichen gelegene, Punkte Pj
(j =1, * - -, s), die sog. markiert, sodann sei T durch ein
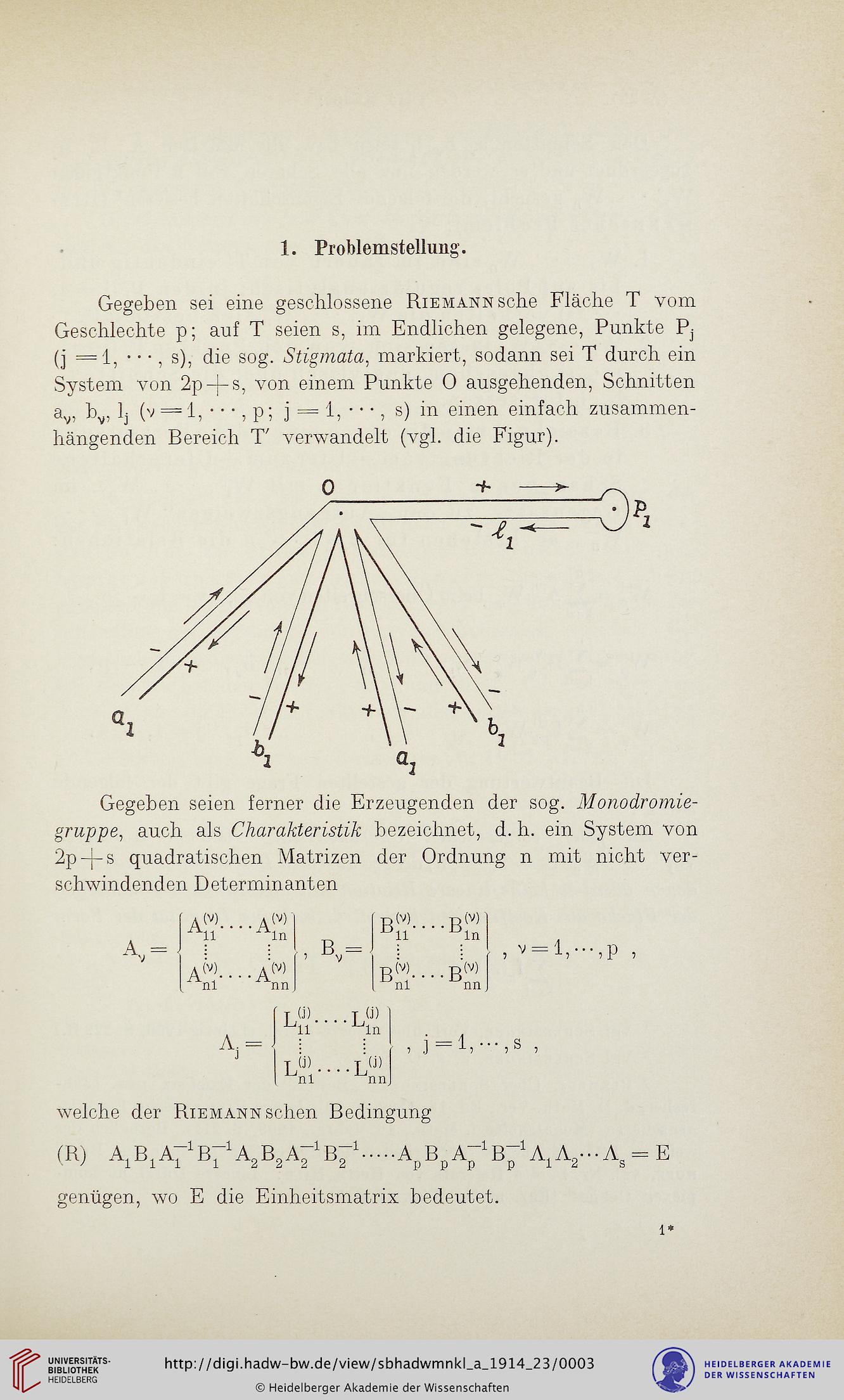
System von 2p-}-s, von einem Punkte 0 ausgehenden, Schnitten
a^, Fj, lj (v = 1, - - -, p; j = 1, ''', s) in einen einfach zusammen-
hängenden Bereich T' verwandelt (vgl. die Figur).
Gegeben seien ferner die Erzeugenden der sog.
gruppe, auch als bezeichnet, d. h. ein System von
2p-j-s quadratischen Matrizen der Ordnung n mit nicht ver-
schwindenden Determinanten
A^)..
"hi
. AM
- B,-
Rn"
"B^
^nl
..AM
nn
TD M
Rnl"
-sh
Aj= .
y(j)
ft"
T (j)
"d"
TÜ)
^nl"
T(j)
nn
welche der RiEMANN sehen Bedingung
(R) A,B,ApB-'A,B,A-'Bp.A,B,ApB-'A,A,...A, = E
genügen, wo E die Einheitsmatrix bedeutet.
l
Gegeben sei eine geschlossene RiEMANNSche Fläche T vom
Geschlechte p; auf T seien s, im Endlichen gelegene, Punkte Pj
(j =1, * - -, s), die sog. markiert, sodann sei T durch ein
System von 2p-}-s, von einem Punkte 0 ausgehenden, Schnitten
a^, Fj, lj (v = 1, - - -, p; j = 1, ''', s) in einen einfach zusammen-
hängenden Bereich T' verwandelt (vgl. die Figur).
Gegeben seien ferner die Erzeugenden der sog.
gruppe, auch als bezeichnet, d. h. ein System von
2p-j-s quadratischen Matrizen der Ordnung n mit nicht ver-
schwindenden Determinanten
A^)..
"hi
. AM
- B,-
Rn"
"B^
^nl
..AM
nn
TD M
Rnl"
-sh
Aj= .
y(j)
ft"
T (j)
"d"
TÜ)
^nl"
T(j)
nn
welche der RiEMANN sehen Bedingung
(R) A,B,ApB-'A,B,A-'Bp.A,B,ApB-'A,A,...A, = E
genügen, wo E die Einheitsmatrix bedeutet.
l