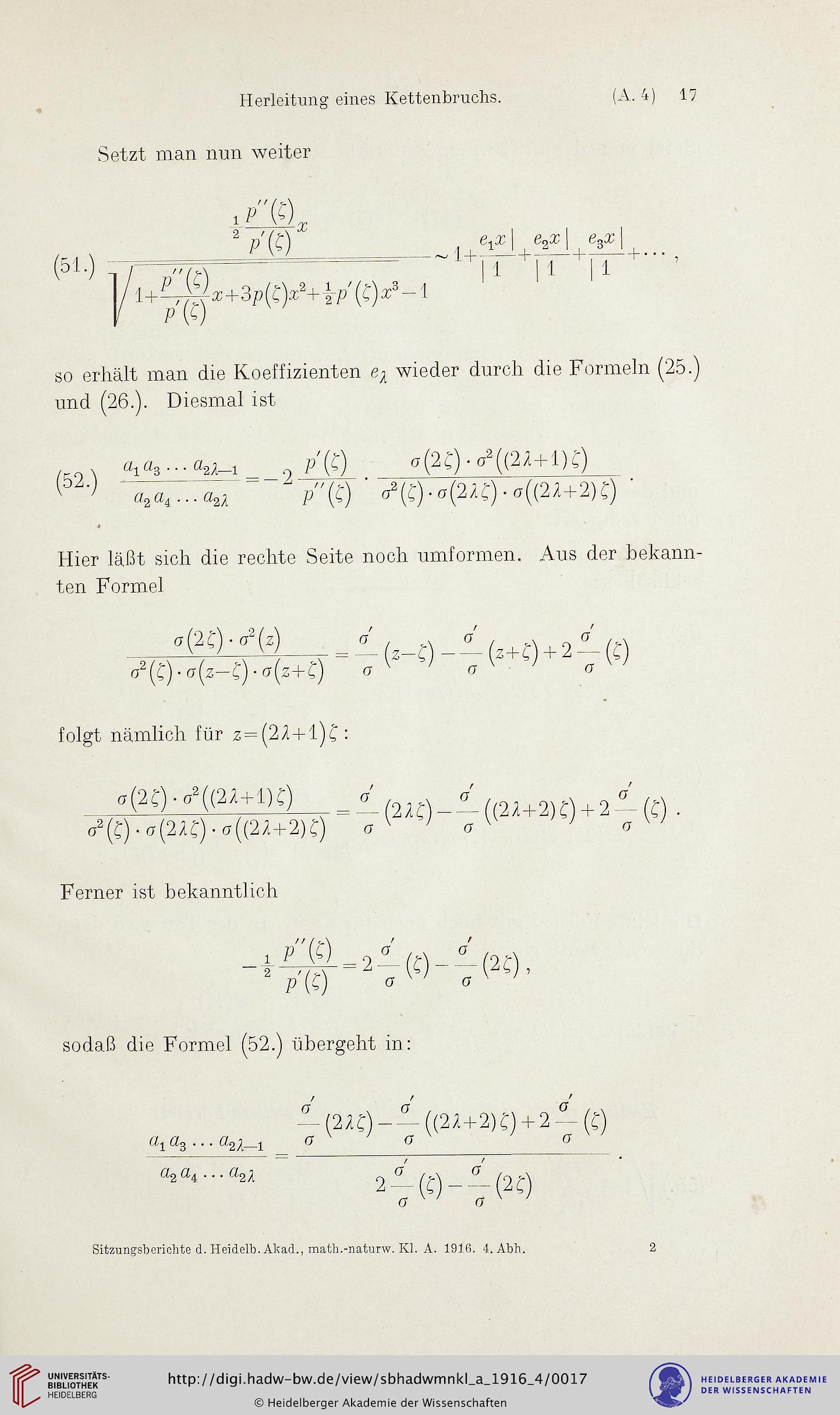Herleitung eines Kettenbruchs.
(A.4) 17
Setzt man nun weiter
(51.)
i 2 (*)
r
so erhält man die Koeffizienten wieder durch die Formeln (25.)
und (26.). Diesmal ist
(7('2^).o^((21+l)^
*- ^ p"(^) ' ^C)..(2^)..((22+2)^) '
Hier läßt sich die rechte Seite noch umformen. Aus der bekann-
ten Formel
(7 (2^) - 0^(2)
o^(^)-u(z-^)-n(z+^)
folgt nämlich für z = (27+'i)^:
u(2Q.^((22+l)^)
^(^).u(22Q.u((22+2)^) "
= *2 Ab - 2 t+b + ^ 2 t)
(21^)- --((21+2)^) + 2 C(^)
Ferner ist bekanntlich
i ?"(b
2, (b-2-(^).
sodaß die Formel (52.) übergeht in:
j(2n-)---((2^+2)^ + 2-"-(4)
^1 ^3 - - - ^27—1
^2 ^4 - - - ^27
Sitzungsberichte d.Heideib.AkAd.,math.-naturw.K], A. 1916. 4. Abb.
2
(A.4) 17
Setzt man nun weiter
(51.)
i 2 (*)
r
so erhält man die Koeffizienten wieder durch die Formeln (25.)
und (26.). Diesmal ist
(7('2^).o^((21+l)^
*- ^ p"(^) ' ^C)..(2^)..((22+2)^) '
Hier läßt sich die rechte Seite noch umformen. Aus der bekann-
ten Formel
(7 (2^) - 0^(2)
o^(^)-u(z-^)-n(z+^)
folgt nämlich für z = (27+'i)^:
u(2Q.^((22+l)^)
^(^).u(22Q.u((22+2)^) "
= *2 Ab - 2 t+b + ^ 2 t)
(21^)- --((21+2)^) + 2 C(^)
Ferner ist bekanntlich
i ?"(b
2, (b-2-(^).
sodaß die Formel (52.) übergeht in:
j(2n-)---((2^+2)^ + 2-"-(4)
^1 ^3 - - - ^27—1
^2 ^4 - - - ^27
Sitzungsberichte d.Heideib.AkAd.,math.-naturw.K], A. 1916. 4. Abb.
2