Summen und Differenzen ungerader Primzahlen. I. (A. 15) 33
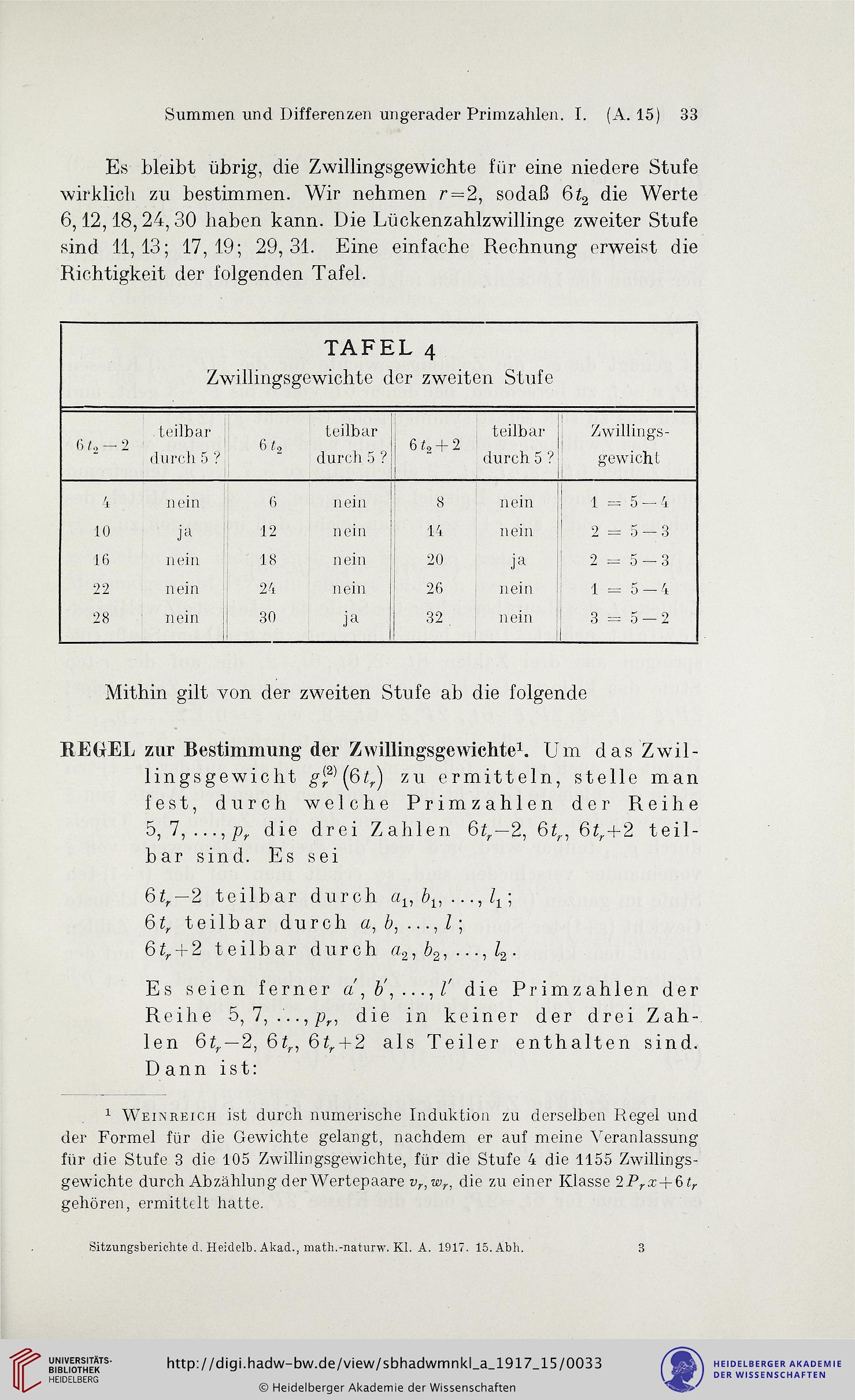
Es bleibt übrig, die Zwillingsgewichte für eine niedere Stufe
wirklich zu bestimmen. Wir nehmen r = 2, sodaß 6^ die Werte
6,12,18, 24, 30 haben kann. Die Lückenzahlzwillinge zweiter Stufe
sind 11,13; 17,19; 29,31. Eine einfache Rechnung erweist die
Richtigkeit der folgenden Tafel.
TAFEL 4
Zwiilingsgcwichte der zweiten Stufe
teilbar
teilbar
teilbar ! Zwillings-
<; — 2
6 G
6/„ + 2
d nrch 5 ?
durch 5 ?
durchs? gewichl
4
nein 6
.
nein
8
nein : 1 = 5 — 4
10
ja 12
nein
14
nein ' 2 = 5 — 3
16
nein 18
nein
20
!!
22
nein 24
nein
26
nein 1 = 5 — 4
28
nein !! 30
ja
32
nein 3 = 5 — 2
!i
Mithin gilt von der zweiten Stufe ab die folgende
RE (TEL zur Bestimmung der Xwillingsgewiehteb Um das Zwil-
lingsgewicht zu ermitteln, stelle man
fest, durch welche Primzahlen der Reihe
5, 7, ...,p, die drei Zahlen 6^—2, 6^, 6^ + 2 teil-
bar sind. Es sei
6f,—2 teilbar durch %i,
6 f, teilbar durch a, ..., ^ ;
6 f, -t- 2 teilbar durch ^^, ..., ^ .
Es seien ferner a', die Primzahlen der
Reihe 5, 7, ...,p,, die in keiner der drei Zah-
len 6%, —2, 6f,, 6f, + 2 als Teiler enthalten sind.
Dann ist:
i WEiiSREiCH ist durch numerische Induktion zu derselben Regel und
der Formel für die Gewichte gelangt, nachdem er auf meine Veranlassung
für die Stufe 3 die 105 Zwillingsgewichte, für die Stufe 4 die 1155 Zwillings-
gewichte durch Abzählung derWertepaare w,, die zu einer Klasse 2P,.;x + 6t,
gehören, ermittelt hatte.
3
Es bleibt übrig, die Zwillingsgewichte für eine niedere Stufe
wirklich zu bestimmen. Wir nehmen r = 2, sodaß 6^ die Werte
6,12,18, 24, 30 haben kann. Die Lückenzahlzwillinge zweiter Stufe
sind 11,13; 17,19; 29,31. Eine einfache Rechnung erweist die
Richtigkeit der folgenden Tafel.
TAFEL 4
Zwiilingsgcwichte der zweiten Stufe
teilbar
teilbar
teilbar ! Zwillings-
<; — 2
6 G
6/„ + 2
d nrch 5 ?
durch 5 ?
durchs? gewichl
4
nein 6
.
nein
8
nein : 1 = 5 — 4
10
ja 12
nein
14
nein ' 2 = 5 — 3
16
nein 18
nein
20
!!
22
nein 24
nein
26
nein 1 = 5 — 4
28
nein !! 30
ja
32
nein 3 = 5 — 2
!i
Mithin gilt von der zweiten Stufe ab die folgende
RE (TEL zur Bestimmung der Xwillingsgewiehteb Um das Zwil-
lingsgewicht zu ermitteln, stelle man
fest, durch welche Primzahlen der Reihe
5, 7, ...,p, die drei Zahlen 6^—2, 6^, 6^ + 2 teil-
bar sind. Es sei
6f,—2 teilbar durch %i,
6 f, teilbar durch a, ..., ^ ;
6 f, -t- 2 teilbar durch ^^, ..., ^ .
Es seien ferner a', die Primzahlen der
Reihe 5, 7, ...,p,, die in keiner der drei Zah-
len 6%, —2, 6f,, 6f, + 2 als Teiler enthalten sind.
Dann ist:
i WEiiSREiCH ist durch numerische Induktion zu derselben Regel und
der Formel für die Gewichte gelangt, nachdem er auf meine Veranlassung
für die Stufe 3 die 105 Zwillingsgewichte, für die Stufe 4 die 1155 Zwillings-
gewichte durch Abzählung derWertepaare w,, die zu einer Klasse 2P,.;x + 6t,
gehören, ermittelt hatte.
3