Über die Schlacke der Clausthaler Silberhütte. (A. 14) 7
tumsstörungen stark unterworfenem Material durch Anwendung
der WüLFiNGSchen Häufungsmethodeh Die Kristalle des Eisen-
kalkzinkolivins bilden ein ausgezeichnetes Beispiel für die zweite
Hälfte der acht WüLFiNGSchen Fälle (a.a. 0. S.6), wo es ein relativ
guter Beobachter mit relativ schlechten Objekten zu tun hat,
und wo WÜLFING Häufung der Beobachtungen und dann hei
eingetretener Häufung der Werte die Streichung der extremen
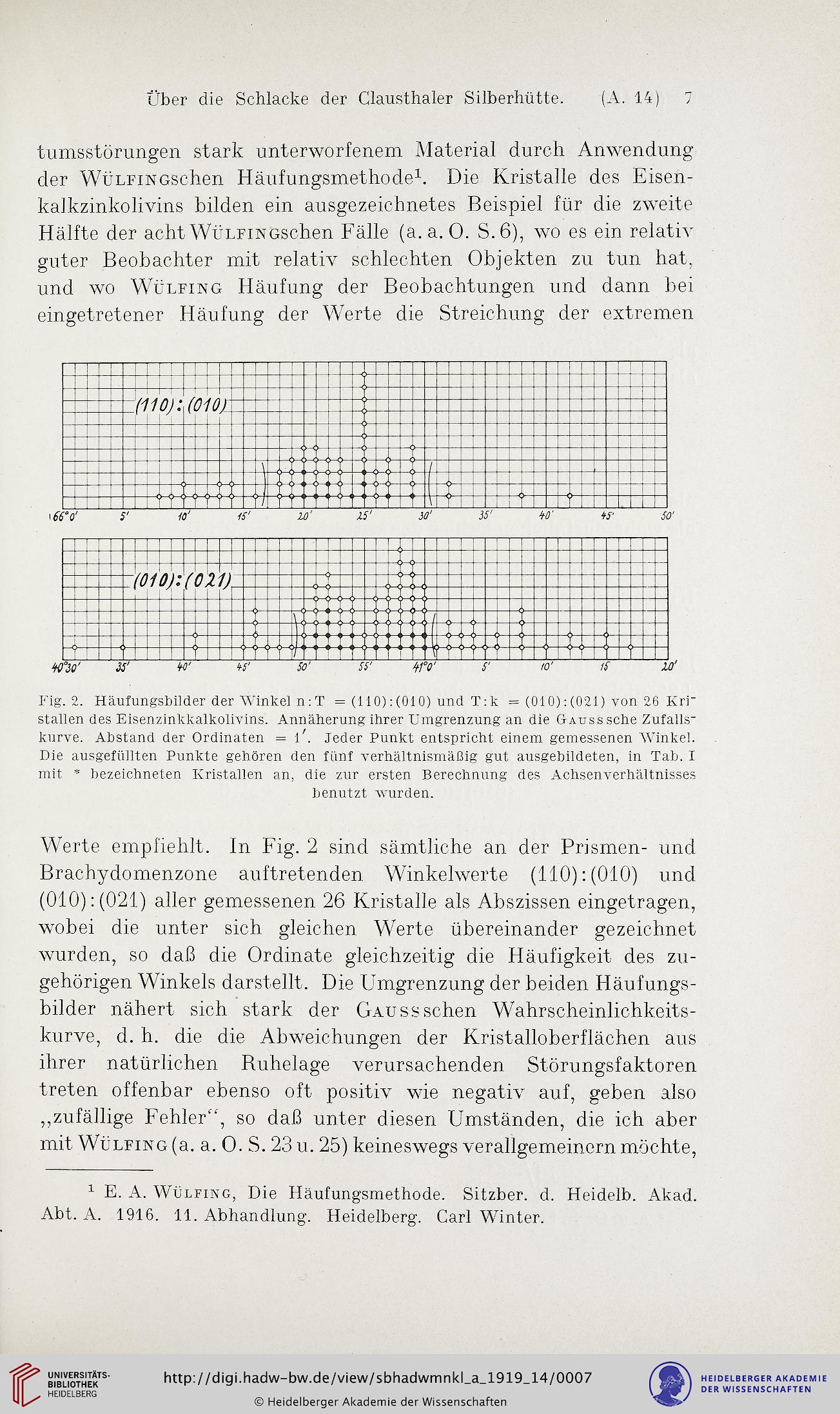
Fig.2. Häufungsbilder derWinkeln:T = (tl0):(010)undT:k =(010):(021)von 26 Kri-
stallen des Eisenzinkkalkolivins. Annäherung ihrer Umgrenzung an die &Auss sehe Zufalls-
kurve. Abstand der Ordinaten = l'. Jeder Punkt entspricht einem gemessenen Winkel.
Die ausgefüllten Punkte gehören den fünf verhältnismäßig gut ausgebildeten, in Tab. I
mit * bezeichneten Kristallen an, die zur ersten Berechnung des Achsenverhältnisses
Werte empfiehlt. In Fig. 2 sind sämtliche an der Prismen- und
Brachydomenzone auftretenden Winkelwerte (If0):(0f0) und
(0i0):(02i) aller gemessenen 26 Kristalle als Abszissen eingetragen,
wobei die unter sich gleichen Werte übereinander gezeichnet
wurden, so daß die Ordinate gleichzeitig die Häufigkeit des zu-
gehörigen Winkels darstellt. Die Fhngrenzung der beiden Häufungs-
bilder nähert sich stark der Ovusssehen Wahrscheinlichkeits-
kurve, d. h. die die Abweichungen der Kristalloberflächen aus
ihrer natürlichen Ruhelage verursachenden Störungsfaktoren
treten offenbar ebenso oft positiv wie negativ auf, geben also
,,zufällige Fehler", so daß unter diesen Umständen, die ich aber
mit WÜLFING (a. a. 0. S. 23 u. 25) keineswegs verallgemeinern möchte,
i E. A. WüLFtNG, Die Häufungsmethode. Sitzber. d. Heidelb. Akad.
Abt. A. 1916. 11. Abhandlung. Heidelberg. Carl Winter.
tumsstörungen stark unterworfenem Material durch Anwendung
der WüLFiNGSchen Häufungsmethodeh Die Kristalle des Eisen-
kalkzinkolivins bilden ein ausgezeichnetes Beispiel für die zweite
Hälfte der acht WüLFiNGSchen Fälle (a.a. 0. S.6), wo es ein relativ
guter Beobachter mit relativ schlechten Objekten zu tun hat,
und wo WÜLFING Häufung der Beobachtungen und dann hei
eingetretener Häufung der Werte die Streichung der extremen
Fig.2. Häufungsbilder derWinkeln:T = (tl0):(010)undT:k =(010):(021)von 26 Kri-
stallen des Eisenzinkkalkolivins. Annäherung ihrer Umgrenzung an die &Auss sehe Zufalls-
kurve. Abstand der Ordinaten = l'. Jeder Punkt entspricht einem gemessenen Winkel.
Die ausgefüllten Punkte gehören den fünf verhältnismäßig gut ausgebildeten, in Tab. I
mit * bezeichneten Kristallen an, die zur ersten Berechnung des Achsenverhältnisses
Werte empfiehlt. In Fig. 2 sind sämtliche an der Prismen- und
Brachydomenzone auftretenden Winkelwerte (If0):(0f0) und
(0i0):(02i) aller gemessenen 26 Kristalle als Abszissen eingetragen,
wobei die unter sich gleichen Werte übereinander gezeichnet
wurden, so daß die Ordinate gleichzeitig die Häufigkeit des zu-
gehörigen Winkels darstellt. Die Fhngrenzung der beiden Häufungs-
bilder nähert sich stark der Ovusssehen Wahrscheinlichkeits-
kurve, d. h. die die Abweichungen der Kristalloberflächen aus
ihrer natürlichen Ruhelage verursachenden Störungsfaktoren
treten offenbar ebenso oft positiv wie negativ auf, geben also
,,zufällige Fehler", so daß unter diesen Umständen, die ich aber
mit WÜLFING (a. a. 0. S. 23 u. 25) keineswegs verallgemeinern möchte,
i E. A. WüLFtNG, Die Häufungsmethode. Sitzber. d. Heidelb. Akad.
Abt. A. 1916. 11. Abhandlung. Heidelberg. Carl Winter.