6
Ernst Roeser:
§4.
Die zugeordneten Fünfecke.
Wendet man die Konstruktion entsprechend auf das rechtwinklige
Fünfeck an, so entstehen die sphärischen Seiten alle einzeln. Es ist um
jede Ecke in jeder senkrechten Ebene der Kreis zu beschreiben. Legt
man die Mittelpunkte zusammen, so entsteht ein Kugelsektor, die Kreis-
bogen Schließen sich zum sphärischen Fünfeck, das die fünf Dreiecke
in der bekannten Weise abzulesen gestattet.
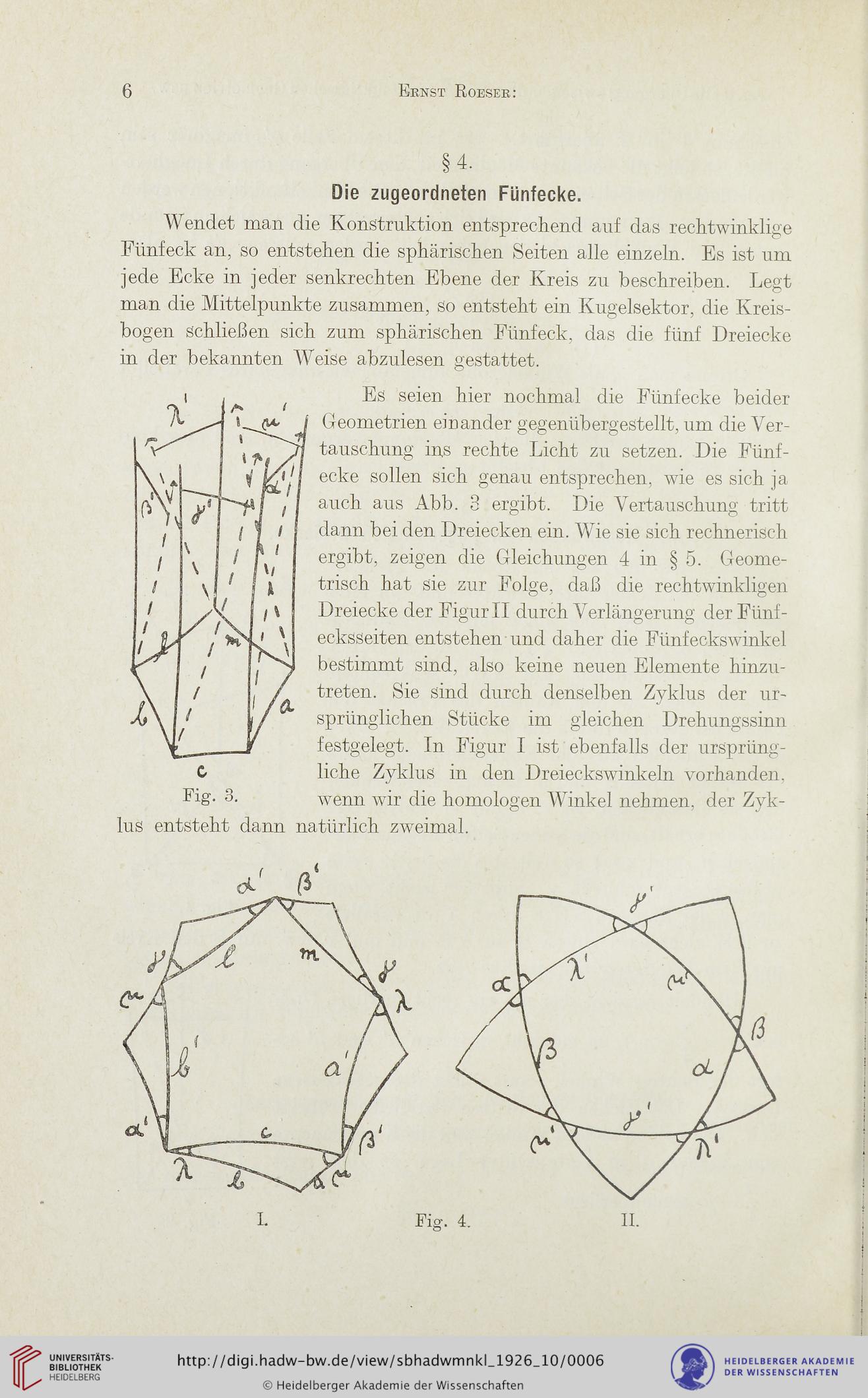
C
Fig. 3.
Es seien hier nochmal die Fünfecke beider
Geometrien einander gegenübergestellt, um die Ver-
tauschung ins rechte Licht zu setzen. Die Fünf-
ecke sollen sich genau entsprechen, wie es sich ja
auch aus Abb. 3 ergibt. Die Vertauschung tritt
dann bei den Dreiecken ein. Wie sie sich rechnerisch
ergibt, zeigen die Gleichungen 4 in § 5. Geome-
trisch hat sie zur Folge, daß die rechtwinkligen
Dreiecke der Figur II durch Verlängerung der Fünf-
ecksseiten entstehen und daher die Fünfeckswinkel
bestimmt sind, also keine neuen Elemente hinzu-
treten. Sie sind durch denselben Zyklus der ur-
sprünglichen Stücke im gleichen Drehungssinn
festgelegt. In Figur I ist ebenfalls der ursprüng-
liche Zyklus in den Dreiecks winkeln vorhanden,
wenn wir die homologen Winkel nehmen, der Zyk-
lus entsteht dann natürlich zweimal.
I.
Fig. 4.
II.
Ernst Roeser:
§4.
Die zugeordneten Fünfecke.
Wendet man die Konstruktion entsprechend auf das rechtwinklige
Fünfeck an, so entstehen die sphärischen Seiten alle einzeln. Es ist um
jede Ecke in jeder senkrechten Ebene der Kreis zu beschreiben. Legt
man die Mittelpunkte zusammen, so entsteht ein Kugelsektor, die Kreis-
bogen Schließen sich zum sphärischen Fünfeck, das die fünf Dreiecke
in der bekannten Weise abzulesen gestattet.
C
Fig. 3.
Es seien hier nochmal die Fünfecke beider
Geometrien einander gegenübergestellt, um die Ver-
tauschung ins rechte Licht zu setzen. Die Fünf-
ecke sollen sich genau entsprechen, wie es sich ja
auch aus Abb. 3 ergibt. Die Vertauschung tritt
dann bei den Dreiecken ein. Wie sie sich rechnerisch
ergibt, zeigen die Gleichungen 4 in § 5. Geome-
trisch hat sie zur Folge, daß die rechtwinkligen
Dreiecke der Figur II durch Verlängerung der Fünf-
ecksseiten entstehen und daher die Fünfeckswinkel
bestimmt sind, also keine neuen Elemente hinzu-
treten. Sie sind durch denselben Zyklus der ur-
sprünglichen Stücke im gleichen Drehungssinn
festgelegt. In Figur I ist ebenfalls der ursprüng-
liche Zyklus in den Dreiecks winkeln vorhanden,
wenn wir die homologen Winkel nehmen, der Zyk-
lus entsteht dann natürlich zweimal.
I.
Fig. 4.
II.