8
Ernst Roeser:
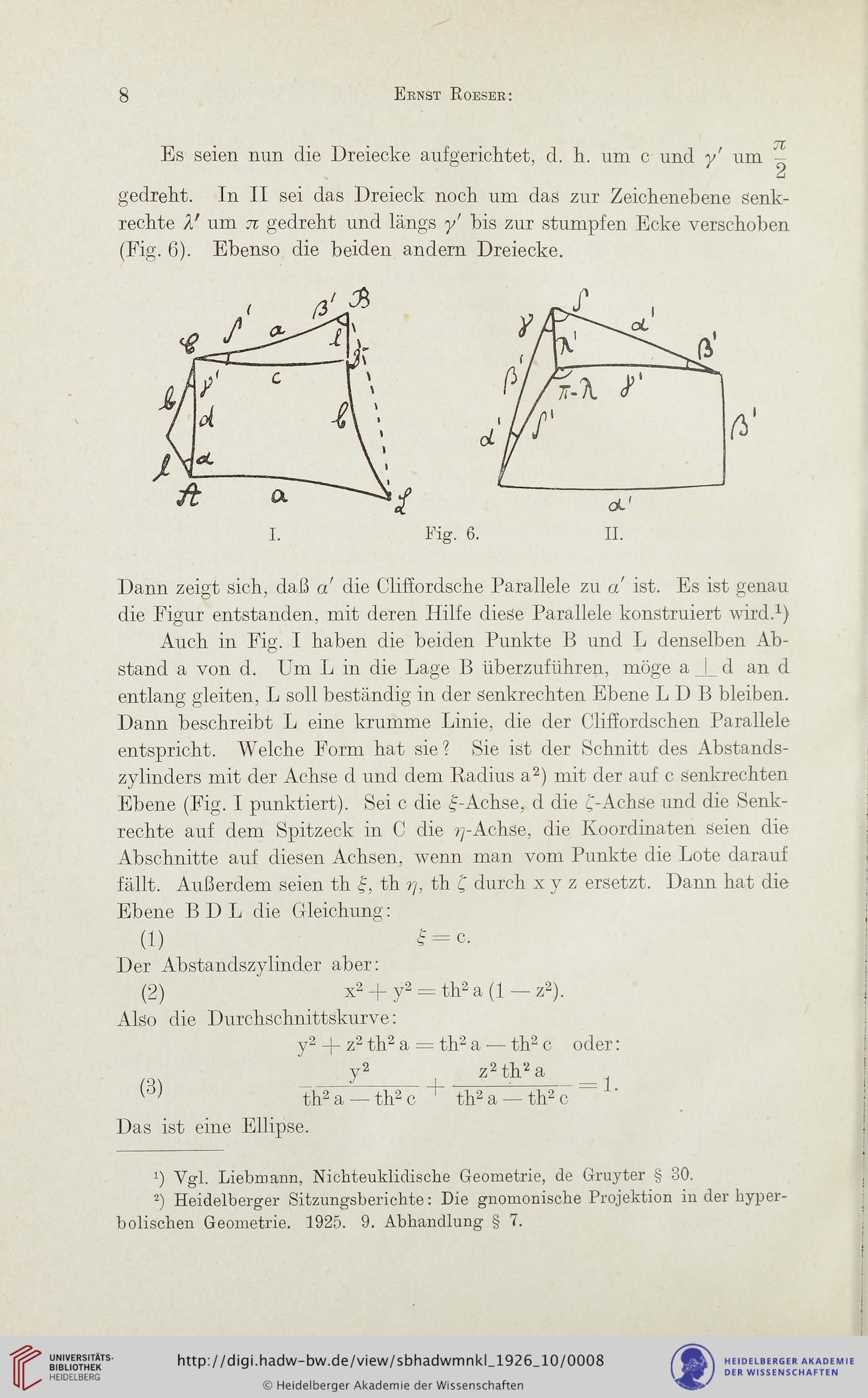
Es seien nun die Dreiecke aufgerichtet, d. h. um c und y' um -
gedreht. In II sei das Dreieck noch um das zur Zeichenebene senk-
rechte U um n gedreht und längs y' bis zur stumpfen Ecke verschoben
(Fig. 6). Ebenso die beiden andern Dreiecke.
Dann zeigt sich, daß a die Cliffordsche Parallele zu a ist. Es ist genau
die Figur entstanden, mit deren Hilfe diese Parallele konstruiert wird.1)
Auch in Fig. I haben die beiden Punkte B und L denselben Ab-
stand a von d. Um L in die Lage B überzuführen, möge a I d an d
entlang gleiten, L soll beständig in der senkrechten Ebene L D B bleiben.
Dann beschreibt L eine krumme Linie, die der Cliffordschen Parallele
entspricht. Welche Form hat sie? Sie ist der Schnitt des Abstands-
zylinders mit der Achse d und dem Radius a2) mit der auf c senkrechten
Ebene (Fig. I punktiert). Sei c die £-Achse, d die £-Achse und die Senk-
rechte auf dem Spitzeck in C die ?;-Achse, die Koordinaten Seien die
Abschnitte auf diesen Achsen, wenn man vom Punkte die Lote darauf
fällt. Außerdem seien th £, th ?], th £ durch x y z ersetzt. Dann hat die
Ebene BDL die Gleichung:
(1) . -
Der Abstandszylinder aber:
(2) x2 -j- y2 = th2 a (1 — z2).
Also die Durchschnittskurve:
y2 + z2 th2 a = th2 a — th2 c oder:
_ y2 , z2th‘2a -
’ ' th2 a — th2 c th2 a — th2 c
Das ist eine Ellipse.
x) Vgl. Liebmann, Nichteuklidische Geometrie, de Gruyter § 30.
2) Heidelberger Sitzungsberichte: Die gnomonische Projektion in der hyper-
bolischen Geometrie. 1925. 9. Abhandlung § 7.
Ernst Roeser:
Es seien nun die Dreiecke aufgerichtet, d. h. um c und y' um -
gedreht. In II sei das Dreieck noch um das zur Zeichenebene senk-
rechte U um n gedreht und längs y' bis zur stumpfen Ecke verschoben
(Fig. 6). Ebenso die beiden andern Dreiecke.
Dann zeigt sich, daß a die Cliffordsche Parallele zu a ist. Es ist genau
die Figur entstanden, mit deren Hilfe diese Parallele konstruiert wird.1)
Auch in Fig. I haben die beiden Punkte B und L denselben Ab-
stand a von d. Um L in die Lage B überzuführen, möge a I d an d
entlang gleiten, L soll beständig in der senkrechten Ebene L D B bleiben.
Dann beschreibt L eine krumme Linie, die der Cliffordschen Parallele
entspricht. Welche Form hat sie? Sie ist der Schnitt des Abstands-
zylinders mit der Achse d und dem Radius a2) mit der auf c senkrechten
Ebene (Fig. I punktiert). Sei c die £-Achse, d die £-Achse und die Senk-
rechte auf dem Spitzeck in C die ?;-Achse, die Koordinaten Seien die
Abschnitte auf diesen Achsen, wenn man vom Punkte die Lote darauf
fällt. Außerdem seien th £, th ?], th £ durch x y z ersetzt. Dann hat die
Ebene BDL die Gleichung:
(1) . -
Der Abstandszylinder aber:
(2) x2 -j- y2 = th2 a (1 — z2).
Also die Durchschnittskurve:
y2 + z2 th2 a = th2 a — th2 c oder:
_ y2 , z2th‘2a -
’ ' th2 a — th2 c th2 a — th2 c
Das ist eine Ellipse.
x) Vgl. Liebmann, Nichteuklidische Geometrie, de Gruyter § 30.
2) Heidelberger Sitzungsberichte: Die gnomonische Projektion in der hyper-
bolischen Geometrie. 1925. 9. Abhandlung § 7.