Neue Sätze über sphärische und hyperbolische Fünfecke.
5
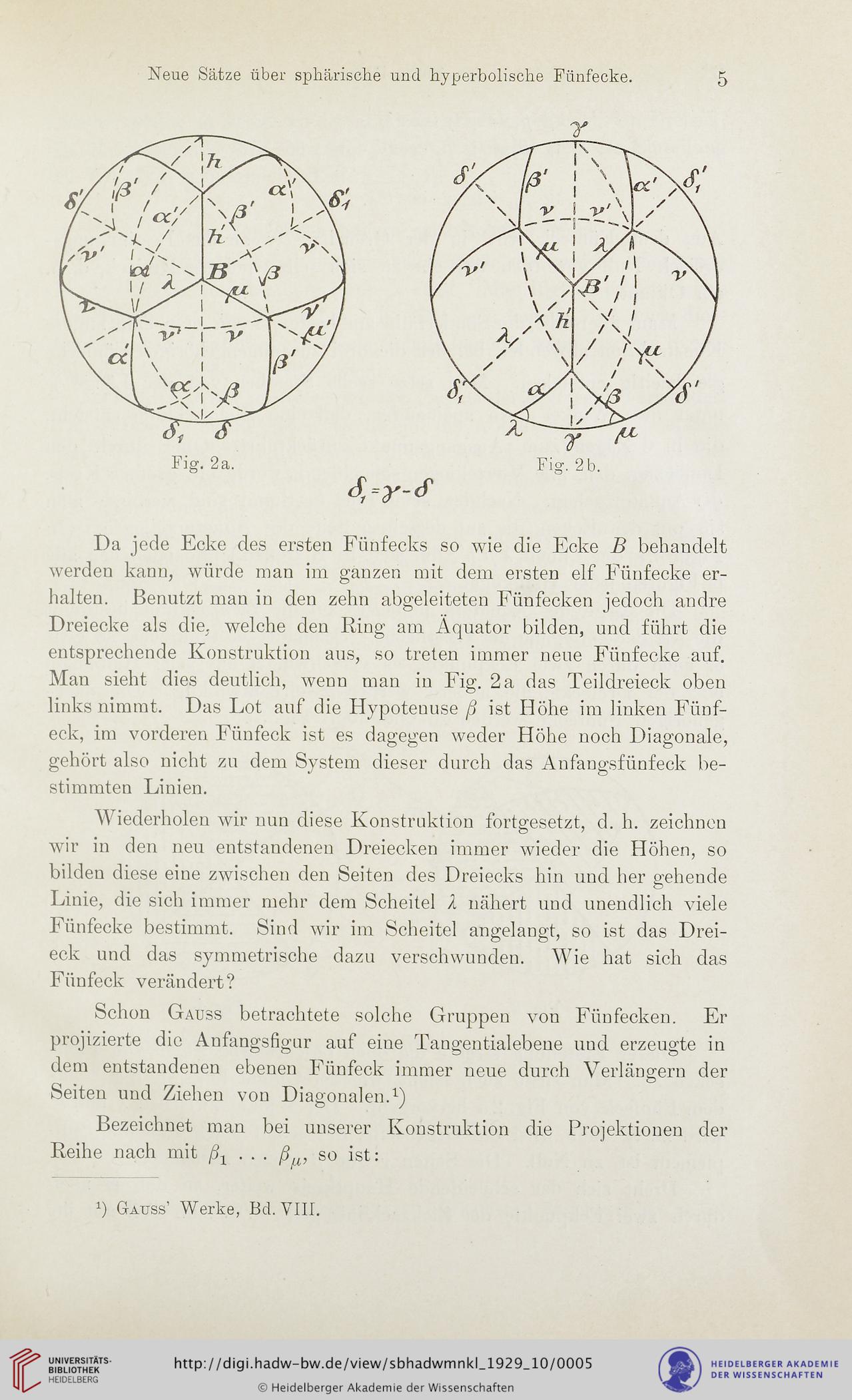
Fig. 2a.
Fig. 2b.
Da jede Ecke des ersten Fünfecks so wie die Ecke B behandelt
werden kann, würde man im ganzen mit dem ersten elf Fünfecke er-
halten. Benutzt man in den zehn abgeleiteten Fünfecken jedoch andre
Dreiecke als die. welche den Ring am Äquator bilden, und führt die
entsprechende Konstruktion aus, so treten immer neue Fünfecke auf.
Man sieht dies deutlich, wenn man in Fig. 2 a das Teildreieck oben
links nimmt. Das Lot auf die Hypotenuse ß ist Höhe im linken Fünf-
eck, im vorderen Fünfeck ist es dagegen weder Höhe noch Diagonale,
gehört also nicht zu dem System dieser durch das Anfangsfünfeck be-
stimmten Linien.
Wiederholen wir nun diese Konstruktion fortgesetzt, d. h. zeichnen
wir in den neu entstandenen Dreiecken immer wieder die Höhen, so
bilden diese eine zwischen den Seiten des Dreiecks hin und her gehende
Linie, die sich immer mehr dem Scheitel 2 nähert und unendlich viele
Fünfecke bestimmt. Sind wir im Scheitel angelangt, so ist das Drei-
eck und das symmetrische dazu verschwunden. Wie hat sich das
Fünfeck verändert?
Schon Gauss betrachtete solche Gruppen von Fünfecken. Er
projizierte die Anfangsfigur auf eine Tangentialebene und erzeugte in
dem entstandenen ebenen Fünfeck immer neue durch Verlängern der
Seiten und Ziehen von Diagonalen.1)
Bezeichnet man bei unserer Konstruktion die Projektionen der
Reihe nach mit ßx . . . ßu, so ist:
x) Gauss’ Werke, Bd. VIII.
5
Fig. 2a.
Fig. 2b.
Da jede Ecke des ersten Fünfecks so wie die Ecke B behandelt
werden kann, würde man im ganzen mit dem ersten elf Fünfecke er-
halten. Benutzt man in den zehn abgeleiteten Fünfecken jedoch andre
Dreiecke als die. welche den Ring am Äquator bilden, und führt die
entsprechende Konstruktion aus, so treten immer neue Fünfecke auf.
Man sieht dies deutlich, wenn man in Fig. 2 a das Teildreieck oben
links nimmt. Das Lot auf die Hypotenuse ß ist Höhe im linken Fünf-
eck, im vorderen Fünfeck ist es dagegen weder Höhe noch Diagonale,
gehört also nicht zu dem System dieser durch das Anfangsfünfeck be-
stimmten Linien.
Wiederholen wir nun diese Konstruktion fortgesetzt, d. h. zeichnen
wir in den neu entstandenen Dreiecken immer wieder die Höhen, so
bilden diese eine zwischen den Seiten des Dreiecks hin und her gehende
Linie, die sich immer mehr dem Scheitel 2 nähert und unendlich viele
Fünfecke bestimmt. Sind wir im Scheitel angelangt, so ist das Drei-
eck und das symmetrische dazu verschwunden. Wie hat sich das
Fünfeck verändert?
Schon Gauss betrachtete solche Gruppen von Fünfecken. Er
projizierte die Anfangsfigur auf eine Tangentialebene und erzeugte in
dem entstandenen ebenen Fünfeck immer neue durch Verlängern der
Seiten und Ziehen von Diagonalen.1)
Bezeichnet man bei unserer Konstruktion die Projektionen der
Reihe nach mit ßx . . . ßu, so ist:
x) Gauss’ Werke, Bd. VIII.