DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.56257#0010
10 (A.3)
L. Heffter und W. Stollenwerk:
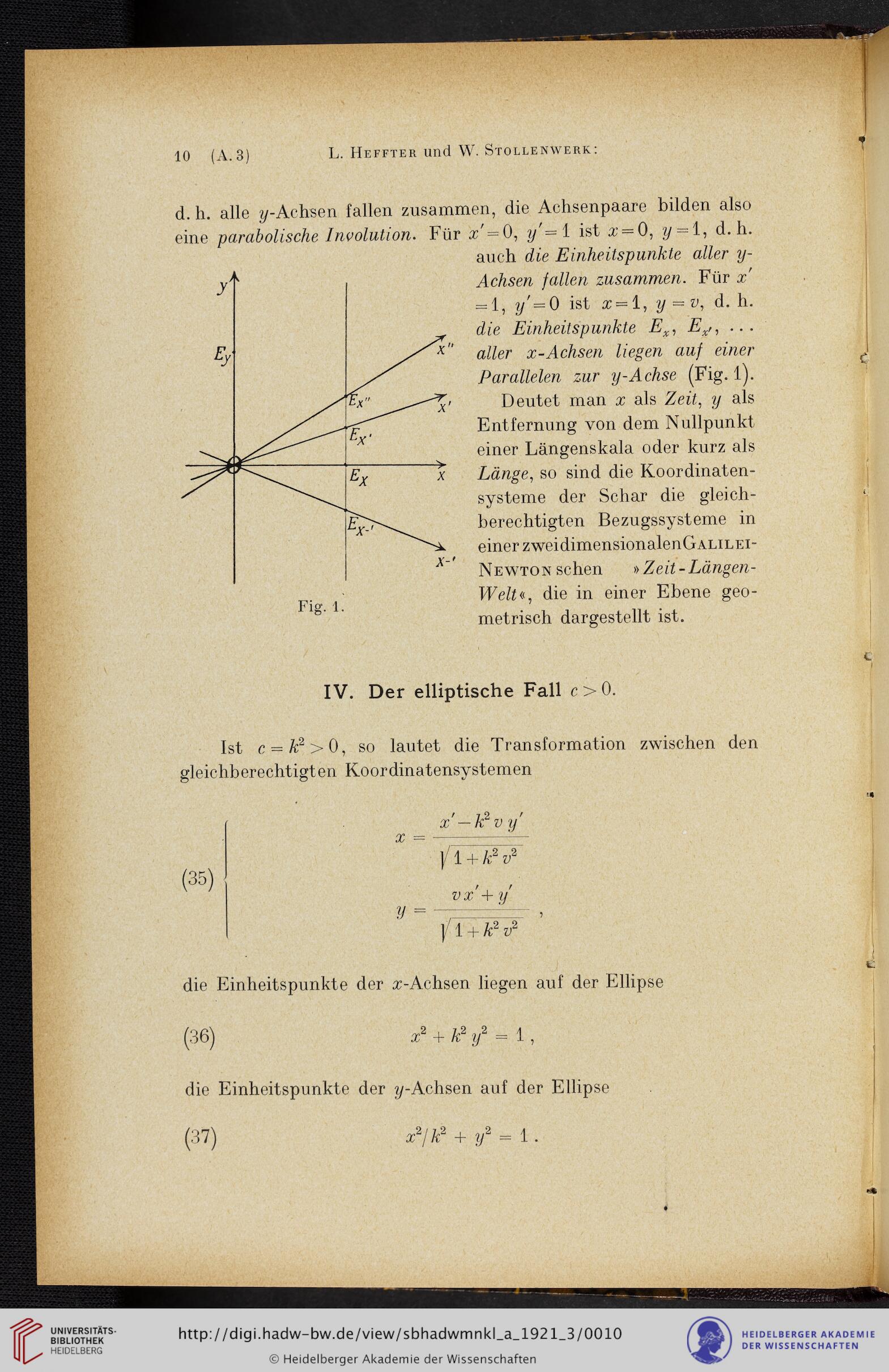
d. h. alle ^/-Achsen fallen zusammen, die Achsenpaare bilden also
eine parabolische Involution. Für z'=0, y'=i ist ,r = 0, y = l, d. h.
auch die Einheitspunkte aller y-
Achsen fallen zusammen. Für x
= 1, y,=0 ist x~l, y = v, d. h.
die Einheitspunkte Ex, Ex,, ...
aller x-Achsen liegen auf einer
Parallelen zur y-Achse (Fig. 1).
Deutet man x als Zeit, y als
Entfernung von dem Nullpunkt
einer Längenskala oder kurz als
Länge, so sind die Koordinaten-
systeme der Schar die gleich-
berechtigten Bezugssysteme in
einer zweidimensionalenGALiLEi-
Newton sehen »Zeit-Längen-
Welt«, die in einer Ebene geo-
metrisch dargestellt ist.
IV. Der elliptische Fall c>0.
(35)
die Einheitspunkte der rc-Achsen liegen auf der Ellipse
(36)
die Einheitspunkte der ?/-Achsen auf der Ellipse
(37)
x2/k2 + y2 = 1.
x2 + k2 y2 = 1,
Ist c = k2 > 0, so lautet die Transformation zwischen den
gleichberechtigten Koordinatensystemen
vx'+ y'
y =
x' — k2
x =-
L. Heffter und W. Stollenwerk:
d. h. alle ^/-Achsen fallen zusammen, die Achsenpaare bilden also
eine parabolische Involution. Für z'=0, y'=i ist ,r = 0, y = l, d. h.
auch die Einheitspunkte aller y-
Achsen fallen zusammen. Für x
= 1, y,=0 ist x~l, y = v, d. h.
die Einheitspunkte Ex, Ex,, ...
aller x-Achsen liegen auf einer
Parallelen zur y-Achse (Fig. 1).
Deutet man x als Zeit, y als
Entfernung von dem Nullpunkt
einer Längenskala oder kurz als
Länge, so sind die Koordinaten-
systeme der Schar die gleich-
berechtigten Bezugssysteme in
einer zweidimensionalenGALiLEi-
Newton sehen »Zeit-Längen-
Welt«, die in einer Ebene geo-
metrisch dargestellt ist.
IV. Der elliptische Fall c>0.
(35)
die Einheitspunkte der rc-Achsen liegen auf der Ellipse
(36)
die Einheitspunkte der ?/-Achsen auf der Ellipse
(37)
x2/k2 + y2 = 1.
x2 + k2 y2 = 1,
Ist c = k2 > 0, so lautet die Transformation zwischen den
gleichberechtigten Koordinatensystemen
vx'+ y'
y =
x' — k2
x =-