14
Ernst Roeser
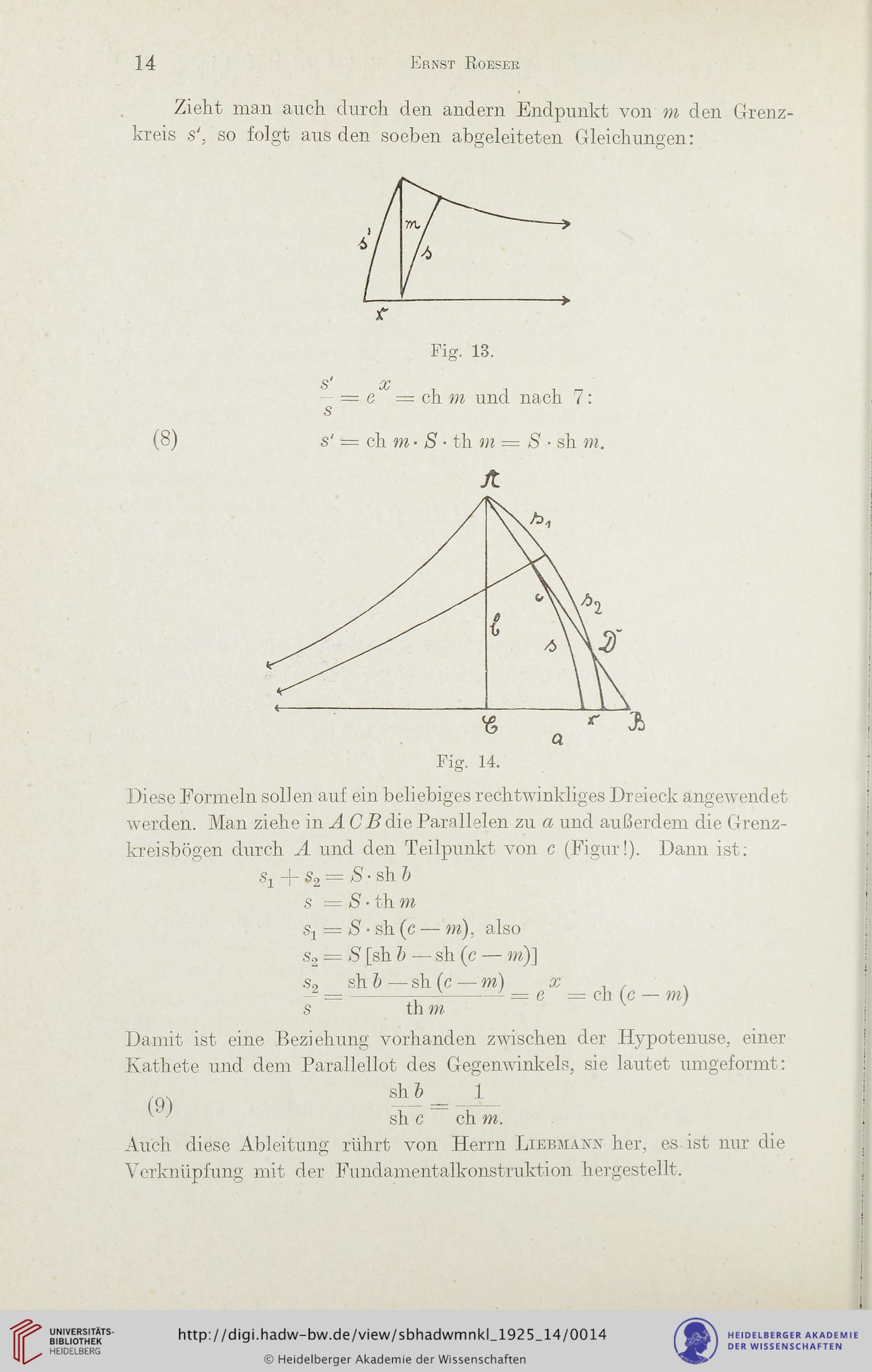
Zieht man auch durch den andern Endpunkt von m den Grenz-
kreis s', so folgt aus den soeben abgeleiteten Gleichungen:
Fig. 13.
- = e = ch m und nach 7:
s
(8) s' = ch m- S • th m — S • sh m.
Diese Formeln sollen auf ein beliebiges rechtwinkliges Dreieck angewendet
werden. Man ziehe in A CT? die Parallelen zu a und außerdem die Grenz-
kreisbögen durch A und den Teilpunkt von c (Figur!). Dann ist;
Sj -L s2 — S • sh b
s = S ■ th m
s1 — S • sh (c — m), also
s2 = S [sh b — sh (c — m)]
s9 sh &—sh (c — m) x . , .
-■? =-;— -- — e — ch (c — m)
s th m
Damit ist eine Beziehung vorhanden zwischen der Hypotenuse, einer
Kathete und dem Parallellot des Gegenwinkels, sie lautet umgeformt:
sh b 1
sh c ch m.
Auch diese Ableitung rührt von Herrn Liebmann her, es. ist nur die
Verknüpfung mit der Fundamentalkonstruktion hergestellt.
Ernst Roeser
Zieht man auch durch den andern Endpunkt von m den Grenz-
kreis s', so folgt aus den soeben abgeleiteten Gleichungen:
Fig. 13.
- = e = ch m und nach 7:
s
(8) s' = ch m- S • th m — S • sh m.
Diese Formeln sollen auf ein beliebiges rechtwinkliges Dreieck angewendet
werden. Man ziehe in A CT? die Parallelen zu a und außerdem die Grenz-
kreisbögen durch A und den Teilpunkt von c (Figur!). Dann ist;
Sj -L s2 — S • sh b
s = S ■ th m
s1 — S • sh (c — m), also
s2 = S [sh b — sh (c — m)]
s9 sh &—sh (c — m) x . , .
-■? =-;— -- — e — ch (c — m)
s th m
Damit ist eine Beziehung vorhanden zwischen der Hypotenuse, einer
Kathete und dem Parallellot des Gegenwinkels, sie lautet umgeformt:
sh b 1
sh c ch m.
Auch diese Ableitung rührt von Herrn Liebmann her, es. ist nur die
Verknüpfung mit der Fundamentalkonstruktion hergestellt.