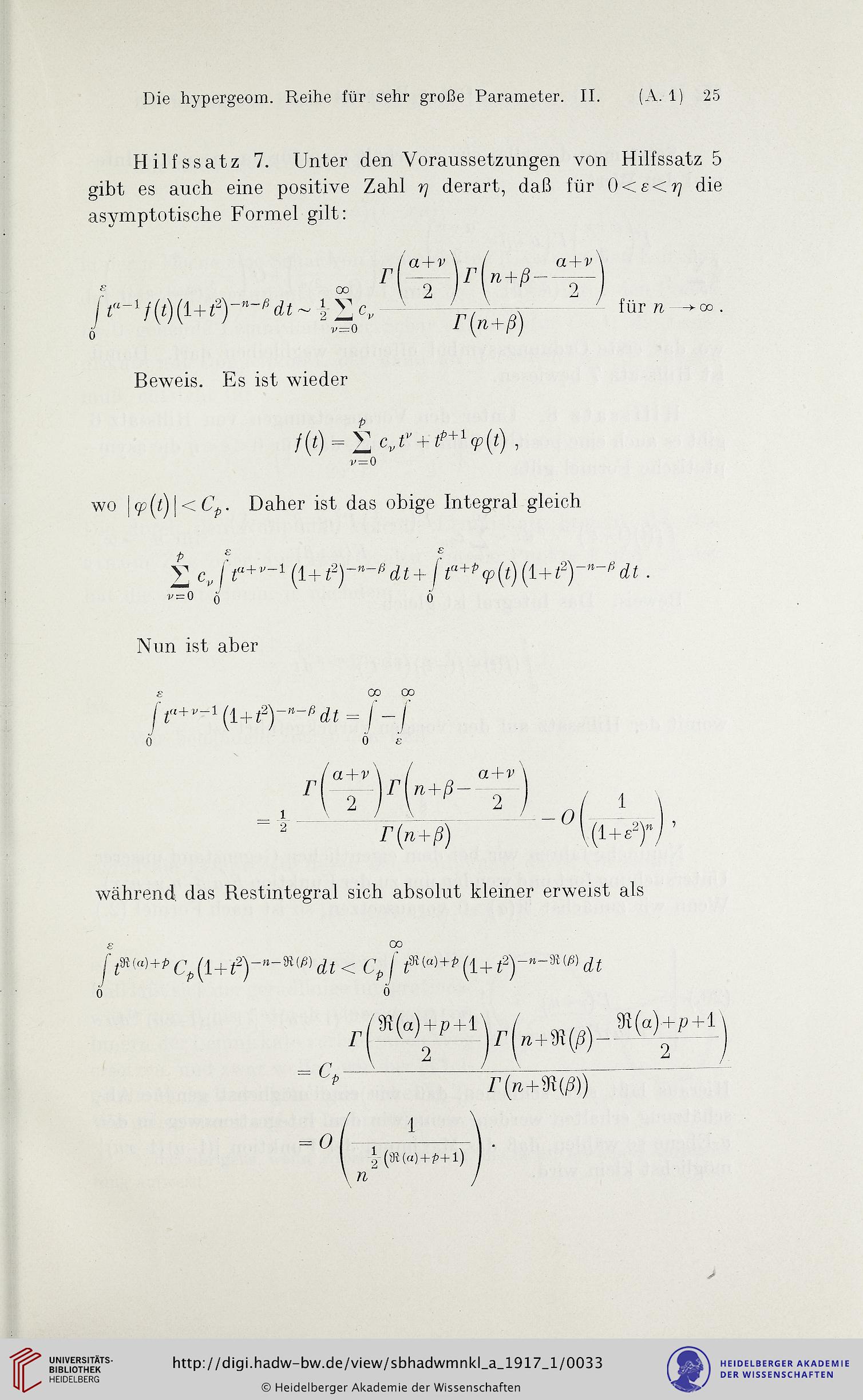DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.36386#0033
Die hypergeom. Reihe für sehr große Parameter. II. (A. 1) 25
Hilfssatz 7. Unter den Voraussetzungen von Hilfssatz 5
gibt es auch eine positive Zahl ^ derart, daß für 0<e<^ die
asymptotische Formel gilt:
^ 00
6
Beweis. Es ist wieder
!' = 0
wo )<p(7)l<Up. Daher ist das obige Integral gleich
V = 0 Q o
Nun ist aber
r
a+r
7' n,+^ —
u + r
0
für n
n+r
a+r
r(n+^)
während das Restintegral sich absolut kleiner erweist als
00
r
/ 91(a)+p+l\
= F.
jrp+9:p)-V")^+t)
r (F+9t(^))
2 (9t(") + ^+l) )
Hilfssatz 7. Unter den Voraussetzungen von Hilfssatz 5
gibt es auch eine positive Zahl ^ derart, daß für 0<e<^ die
asymptotische Formel gilt:
^ 00
6
Beweis. Es ist wieder
!' = 0
wo )<p(7)l<Up. Daher ist das obige Integral gleich
V = 0 Q o
Nun ist aber
r
a+r
7' n,+^ —
u + r
0
für n
n+r
a+r
r(n+^)
während das Restintegral sich absolut kleiner erweist als
00
r
/ 91(a)+p+l\
= F.
jrp+9:p)-V")^+t)
r (F+9t(^))
2 (9t(") + ^+l) )