6
Ernst Roeser
sie senkrecht schneiden. Zwischen den beiden ersten Bündeln und da-
her auch zwischen diesen Geometrien besteht aber ein wesentlicher
Unterschied. Benutzen wir statt der Halbstrahlen die Vollstrahlen, so
gehören zu jedem Punkt der Ebene zwei Punkte der Flächen (auf der
linken Halbkugel bzw. Abstandsfläche noch je ein Punkt). Während
aber alle Punkte der Kugel durch Drehung eines Halbstrahls erreicht
werden können, ist das bei der andern Hälfte der Abstandsfläche nicht
möglich. Das erste Bündel allein vermittelt den Begriff zweier ver-
schiedener Geometrien, das der Voll- und das der HaJbstrahlen.
Trotz dieser Verschiedenheit der Bündel lassen sie sich von einem
s gemeinsamen Gesichtspunkt betrachten, denn sie gehen durch konti-
nuierliche Bewegung ihrer Zentrums in-
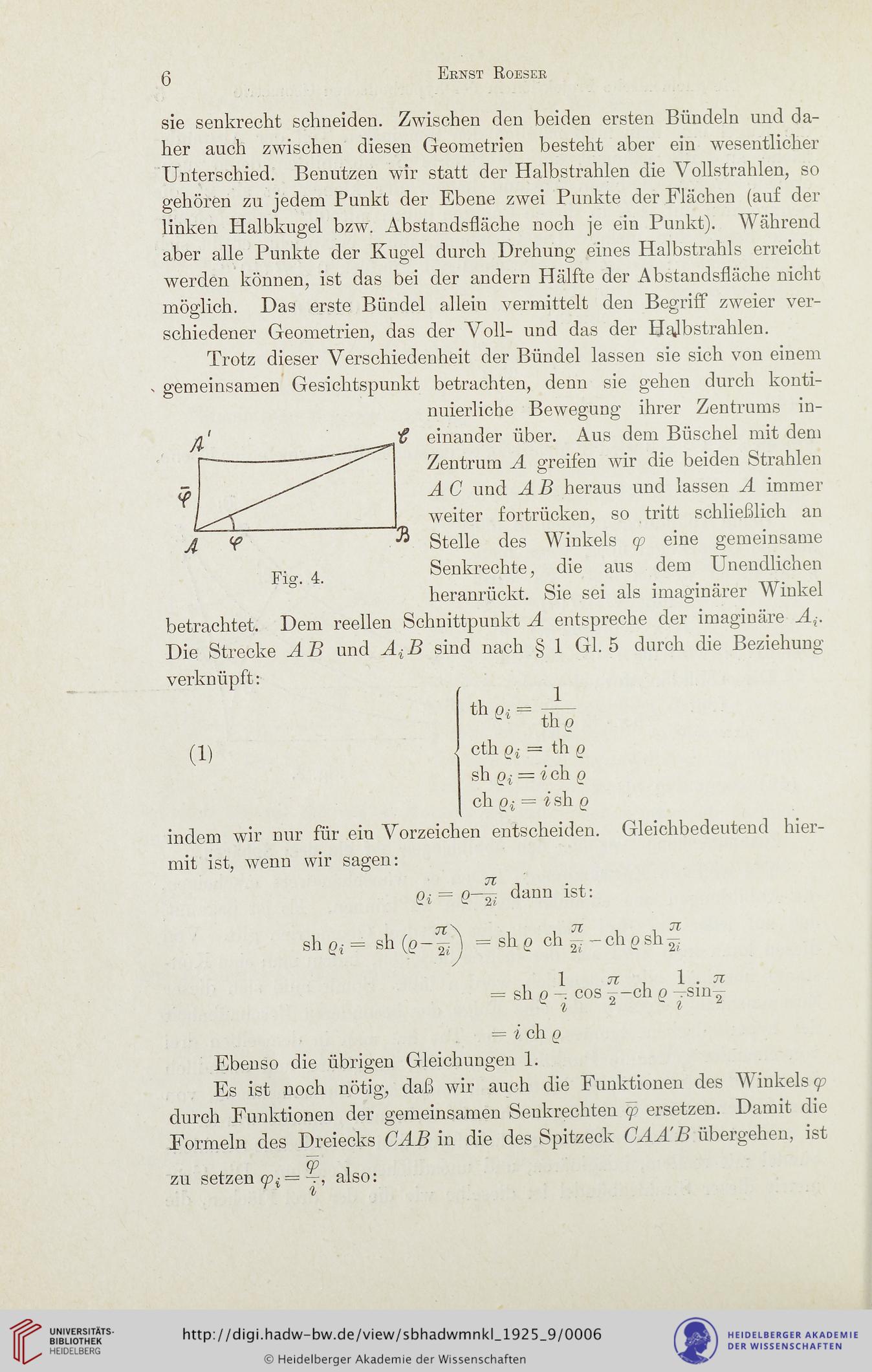
einander über. Aus dem Büschel mit dem
Zentrum A greifen wir die beiden Strahlen
A C und A B heraus und lassen A immer
weiter fortrücken, so tritt schließlich an
Stelle des Winkels cp eine gemeinsame
Senkrechte, die aus dem Unendlichen
heranrückt. Sie sei als imaginärer Winkel
betrachtet. Dem reellen Schnittpunkt A entspreche der imaginäre A{.
Die Strecke AB und sind nach § 1 Gl. 5 durch die Beziehung
verknüpft:
(1)
th Qi -
th q
cth Qi — th Q
sh Pi = ch q
Ai Qi = i sh q
indem wir nur für ein Vorzeichen entscheiden.
Gleichbedeutend hier-
mit ist, wenn wir sagen:
Qi = q—~. dann ist:
sh Qi = sh (p-
, 1 71 . 1 . 71
= sh p — cos y-ch p — SlUy
= i ch p
Ebenso die übrigen Gleichungen 1.
Es ist noch nötig, daß wir auch die Funktionen des Winkels cp
durch Funktionen der gemeinsamen Senkrechten cp ersetzen. Damit die
Formeln des Dreiecks CAB in die des Spitzeck CAA'B übergehen, ist
m i
zu setzen cpi= -r, also:
=shp chg-chpsh^
Ernst Roeser
sie senkrecht schneiden. Zwischen den beiden ersten Bündeln und da-
her auch zwischen diesen Geometrien besteht aber ein wesentlicher
Unterschied. Benutzen wir statt der Halbstrahlen die Vollstrahlen, so
gehören zu jedem Punkt der Ebene zwei Punkte der Flächen (auf der
linken Halbkugel bzw. Abstandsfläche noch je ein Punkt). Während
aber alle Punkte der Kugel durch Drehung eines Halbstrahls erreicht
werden können, ist das bei der andern Hälfte der Abstandsfläche nicht
möglich. Das erste Bündel allein vermittelt den Begriff zweier ver-
schiedener Geometrien, das der Voll- und das der HaJbstrahlen.
Trotz dieser Verschiedenheit der Bündel lassen sie sich von einem
s gemeinsamen Gesichtspunkt betrachten, denn sie gehen durch konti-
nuierliche Bewegung ihrer Zentrums in-
einander über. Aus dem Büschel mit dem
Zentrum A greifen wir die beiden Strahlen
A C und A B heraus und lassen A immer
weiter fortrücken, so tritt schließlich an
Stelle des Winkels cp eine gemeinsame
Senkrechte, die aus dem Unendlichen
heranrückt. Sie sei als imaginärer Winkel
betrachtet. Dem reellen Schnittpunkt A entspreche der imaginäre A{.
Die Strecke AB und sind nach § 1 Gl. 5 durch die Beziehung
verknüpft:
(1)
th Qi -
th q
cth Qi — th Q
sh Pi = ch q
Ai Qi = i sh q
indem wir nur für ein Vorzeichen entscheiden.
Gleichbedeutend hier-
mit ist, wenn wir sagen:
Qi = q—~. dann ist:
sh Qi = sh (p-
, 1 71 . 1 . 71
= sh p — cos y-ch p — SlUy
= i ch p
Ebenso die übrigen Gleichungen 1.
Es ist noch nötig, daß wir auch die Funktionen des Winkels cp
durch Funktionen der gemeinsamen Senkrechten cp ersetzen. Damit die
Formeln des Dreiecks CAB in die des Spitzeck CAA'B übergehen, ist
m i
zu setzen cpi= -r, also:
=shp chg-chpsh^