Summen und Differenzen ungerader Primzahlen, fff. (A. 14) 39
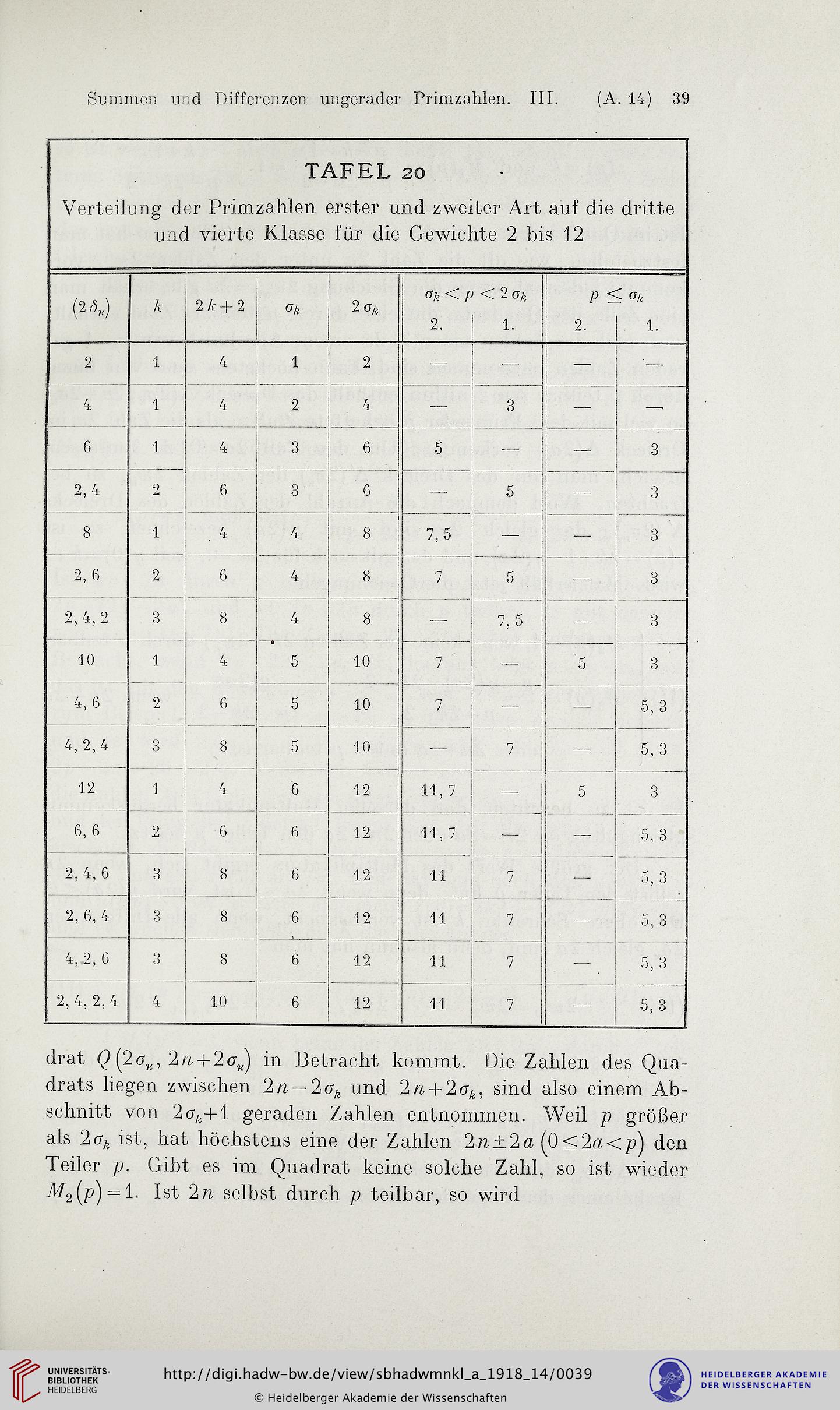
TAFEL 20
Verteilung der Primzahlen erster und zweiter Art auf die dritte
und vierte Klasse für die Gewichte 2 bis 12
(2A.)
A
2A + 2
CA
2 CR
2.
< 2
1.
P <
2.
' 0/;
1.
2
1
4
1
2
—
—
—
4
1
4
2
4
—
3
—
—
6
1
4
3
6
5
—
—
3
2, 4
2
6
3
6
—
5
-
g
8
1
4
4
8
7,5
—
3
2, 6
2
6
4
8
7
5
—
3
2, 4, 2
3
8
4
8
—
7, 5
—
3
10
i
4
'
10
7
—
5
3
4, 6
2
6
5
10
7
—
5, 3
4, 2, 4
3
8
5
10
—
—
5, 3
12
1
4
6
12
11, 7
5
3
6, 6
2
6
6
12
11, 7
—
—
5, 3
2,4,6
3
8
6
12
11
7
- -
5, 3
2, 6, 4
3
8
6
12
11
7
—
5,3
4,2, 6
3
8
6
12
11
7
- -
5, 3
2, 4, 2, 4
10
6
12
11
7
5, 3
drat + in Betracht kommt. Die Zahlen des Qua-
drats liegen zwischen 272 —2 <7% und 2 72+ 2(7%, sind also einem Ab-
schnitt von 2o%+l geraden Zahlen entnommen. Weil p größer
als 2c% ist, hat höchstens eine der Zahlen 2n + 2a (0<:2n<p) den
Teiler p. Gibt es im Quadrat keine solche Zahl, so ist wieder
= Ist 2n selbst durch p teilbar, so wird
TAFEL 20
Verteilung der Primzahlen erster und zweiter Art auf die dritte
und vierte Klasse für die Gewichte 2 bis 12
(2A.)
A
2A + 2
CA
2 CR
2.
< 2
1.
P <
2.
' 0/;
1.
2
1
4
1
2
—
—
—
4
1
4
2
4
—
3
—
—
6
1
4
3
6
5
—
—
3
2, 4
2
6
3
6
—
5
-
g
8
1
4
4
8
7,5
—
3
2, 6
2
6
4
8
7
5
—
3
2, 4, 2
3
8
4
8
—
7, 5
—
3
10
i
4
'
10
7
—
5
3
4, 6
2
6
5
10
7
—
5, 3
4, 2, 4
3
8
5
10
—
—
5, 3
12
1
4
6
12
11, 7
5
3
6, 6
2
6
6
12
11, 7
—
—
5, 3
2,4,6
3
8
6
12
11
7
- -
5, 3
2, 6, 4
3
8
6
12
11
7
—
5,3
4,2, 6
3
8
6
12
11
7
- -
5, 3
2, 4, 2, 4
10
6
12
11
7
5, 3
drat + in Betracht kommt. Die Zahlen des Qua-
drats liegen zwischen 272 —2 <7% und 2 72+ 2(7%, sind also einem Ab-
schnitt von 2o%+l geraden Zahlen entnommen. Weil p größer
als 2c% ist, hat höchstens eine der Zahlen 2n + 2a (0<:2n<p) den
Teiler p. Gibt es im Quadrat keine solche Zahl, so ist wieder
= Ist 2n selbst durch p teilbar, so wird