18
Victor Goldschmidt:
Symmetrische und unsymmetrische Harmonie der Formen.
Jede dei’ beiden ist wesentlich für große Gebiete der Kunst. Die
symmetrische Harmonie beherrscht die Renaissance, die unsym-
metrische das Rokoko und die japanische Kunst. Die unsymmetrische
Harmonie gestattet dem schaffenden Künstler freiere Entfaltung durch
willkürliches Einsetzen exzentrischer Massen und harmonischen Aus-
gleich. Symmetrische Harmonie trägt in sich einen hohen Grad
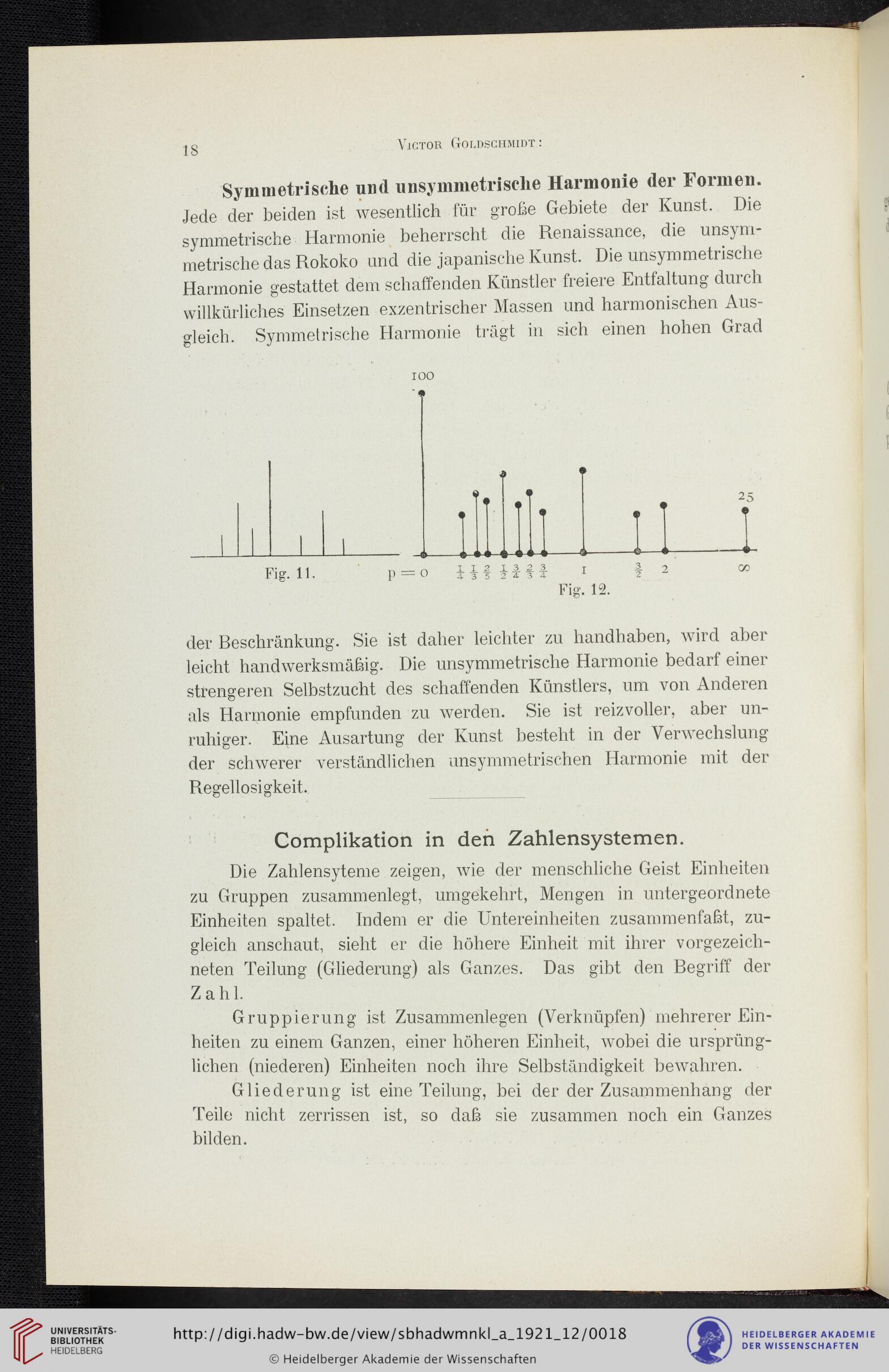
100
■«
Fig. 11. p = o HfHH i < 2 oo
Fig. 12.
der Beschränkung. Sie ist daher leichter zu handhaben, wird aber
leicht handwerksmäßig. Die unsymmetrische Harmonie bedarf einer
strengeren Selbstzucht des schaffenden Künstlers, um von Anderen
als Harinonie empfunden zu werden. Sie ist reizvoller, aber un-
ruhiger. Eine Ausartung der Kunst besteht in der Verwechslung
der schwerer verständlichen unsymmetrischen Harmonie mit der
Regellosigkeit.
Complikation in den Zahlensystemen.
Die Zahlensyteme zeigen, wie der menschliche Geist Einheiten
zu Gruppen zusammenlegt, umgekehrt, Mengen in untergeordnete
Einheiten spaltet. Indem er die Untereinheiten zusammenfaßt, zu-
gleich anschaut, sieht er die höhere Einheit mit ihrer vorgezeich-
neten Teilung (Gliederung) als Ganzes. Das gibt den Begriff der
Zahl.
Gruppierung ist Zusammenlegen (Verknüpfen) mehrerer Ein-
heiten zu einem Ganzen, einer höheren Einheit, wobei die ursprüng-
lichen (niederen) Einheiten noch ihre Selbständigkeit bewahren.
Gliederung ist eine Teilung, bei der der Zusammenhang der
Teile nicht zerrissen ist, so daß sie zusammen noch ein Ganzes
bilden.
Victor Goldschmidt:
Symmetrische und unsymmetrische Harmonie der Formen.
Jede dei’ beiden ist wesentlich für große Gebiete der Kunst. Die
symmetrische Harmonie beherrscht die Renaissance, die unsym-
metrische das Rokoko und die japanische Kunst. Die unsymmetrische
Harmonie gestattet dem schaffenden Künstler freiere Entfaltung durch
willkürliches Einsetzen exzentrischer Massen und harmonischen Aus-
gleich. Symmetrische Harmonie trägt in sich einen hohen Grad
100
■«
Fig. 11. p = o HfHH i < 2 oo
Fig. 12.
der Beschränkung. Sie ist daher leichter zu handhaben, wird aber
leicht handwerksmäßig. Die unsymmetrische Harmonie bedarf einer
strengeren Selbstzucht des schaffenden Künstlers, um von Anderen
als Harinonie empfunden zu werden. Sie ist reizvoller, aber un-
ruhiger. Eine Ausartung der Kunst besteht in der Verwechslung
der schwerer verständlichen unsymmetrischen Harmonie mit der
Regellosigkeit.
Complikation in den Zahlensystemen.
Die Zahlensyteme zeigen, wie der menschliche Geist Einheiten
zu Gruppen zusammenlegt, umgekehrt, Mengen in untergeordnete
Einheiten spaltet. Indem er die Untereinheiten zusammenfaßt, zu-
gleich anschaut, sieht er die höhere Einheit mit ihrer vorgezeich-
neten Teilung (Gliederung) als Ganzes. Das gibt den Begriff der
Zahl.
Gruppierung ist Zusammenlegen (Verknüpfen) mehrerer Ein-
heiten zu einem Ganzen, einer höheren Einheit, wobei die ursprüng-
lichen (niederen) Einheiten noch ihre Selbständigkeit bewahren.
Gliederung ist eine Teilung, bei der der Zusammenhang der
Teile nicht zerrissen ist, so daß sie zusammen noch ein Ganzes
bilden.