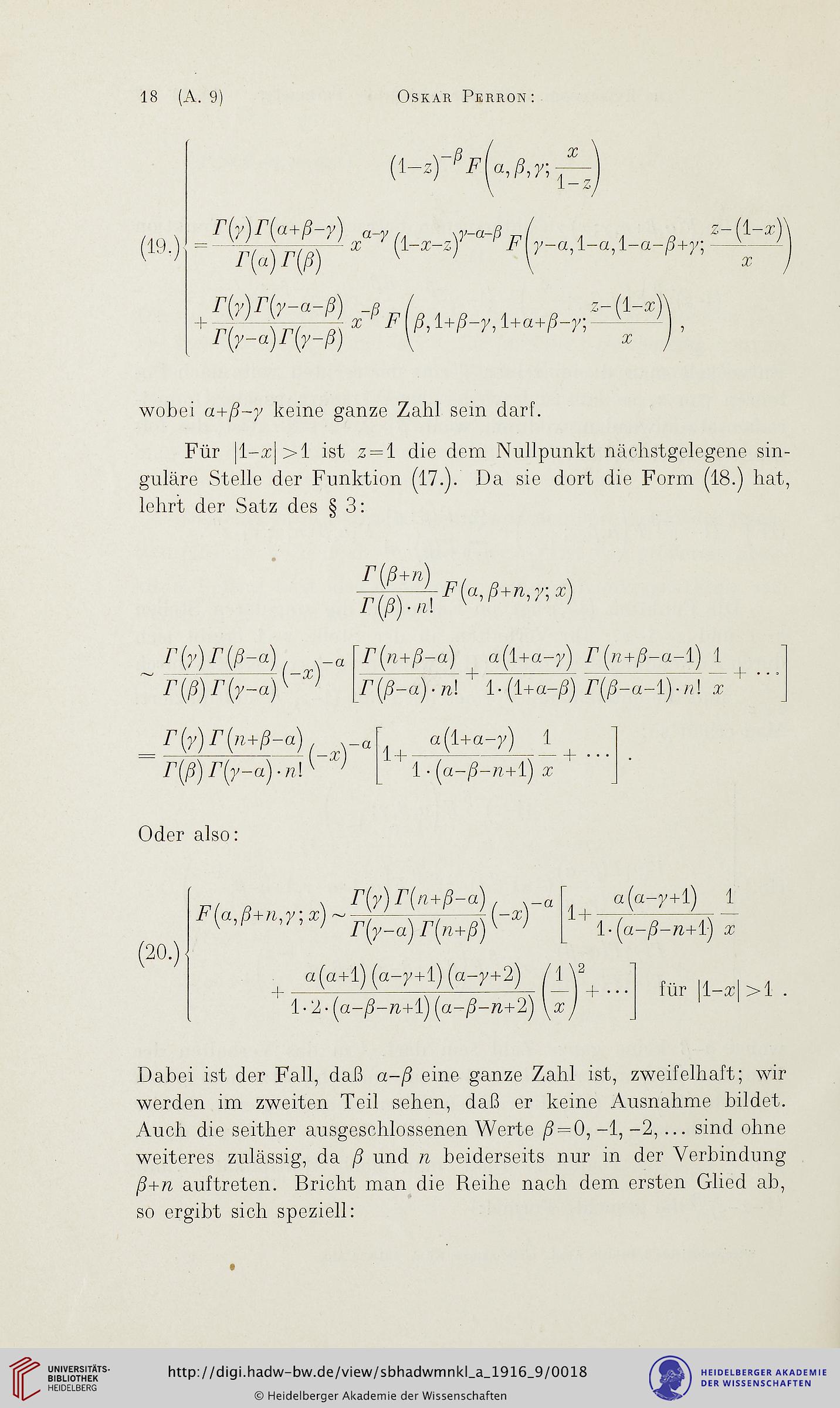DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.34894#0018
18 (A. 9)
OSKAR PERRON:
(19.)
3?
Wz
(i-)^^,y;
3^" ^ (1-3^-z)^ ° ^F^p-a,l-ct,l-a-)9+p;
3? ''" /'* (/?, 1+^-y, l+a+)5-y; — -- - -
wobei a+)$-y keine ganze Zahl sein darf.
Für ist z = l die dem Nullpunkt nächstgelegene sin-
guläre Stelle der Funktion (17.). Da sie dort die Form (18.) hat,
lehrt der Satz des § 3:
f^+T?)
F(.,
^+n,y; z)
r(y)f(^-a), s-nU(H+^-a) a(l+a-y) f(n+^-m-l) 1
rpjr(y-a)'^ l.(l+a-^) r(^-a-l).;:! 7
f(y)r(K+^-a) .-cf a(l+a-y) 1
F(/?)F(y-a)-7?W ^ l-(a-^-^+l)3?
Oder also:
(20.)
F(a,^+77,p; 3:)
r(y)r(n+^-n) ^ L ^(a-p+l) ^
r(p-a)F(n+)5)^ ^ l-(a-^-7Z+l)3?
(a+1) (a-y+l) (a-p+2) /IV
1 - 2 - (a-^-71+1) (a-)5-^+2) ^3;/
Dabei ist der Fall, daß a-/? eine ganze Zahl ist, zweifelhaft; wir
werden im zweiten Teil sehen, daß er keine Ausnahme bildet.
Auch die seither ausgeschlossenen Werte /? = 0, -1, -2, ... sind ohne
weiteres zulässig, da /? und 7r beiderseits nur in der Verbindung
^+73 auftreten. Bricht man die Reihe nach dem ersten Glied ab,
so ergibt sich speziell:
OSKAR PERRON:
(19.)
3?
Wz
(i-)^^,y;
3^" ^ (1-3^-z)^ ° ^F^p-a,l-ct,l-a-)9+p;
3? ''" /'* (/?, 1+^-y, l+a+)5-y; — -- - -
wobei a+)$-y keine ganze Zahl sein darf.
Für ist z = l die dem Nullpunkt nächstgelegene sin-
guläre Stelle der Funktion (17.). Da sie dort die Form (18.) hat,
lehrt der Satz des § 3:
f^+T?)
F(.,
^+n,y; z)
r(y)f(^-a), s-nU(H+^-a) a(l+a-y) f(n+^-m-l) 1
rpjr(y-a)'^ l.(l+a-^) r(^-a-l).;:! 7
f(y)r(K+^-a) .-cf a(l+a-y) 1
F(/?)F(y-a)-7?W ^ l-(a-^-^+l)3?
Oder also:
(20.)
F(a,^+77,p; 3:)
r(y)r(n+^-n) ^ L ^(a-p+l) ^
r(p-a)F(n+)5)^ ^ l-(a-^-7Z+l)3?
(a+1) (a-y+l) (a-p+2) /IV
1 - 2 - (a-^-71+1) (a-)5-^+2) ^3;/
Dabei ist der Fall, daß a-/? eine ganze Zahl ist, zweifelhaft; wir
werden im zweiten Teil sehen, daß er keine Ausnahme bildet.
Auch die seither ausgeschlossenen Werte /? = 0, -1, -2, ... sind ohne
weiteres zulässig, da /? und 7r beiderseits nur in der Verbindung
^+73 auftreten. Bricht man die Reihe nach dem ersten Glied ab,
so ergibt sich speziell: