DOI Seite / Zitierlink:
https://doi.org/10.11588/diglit.43680#0026
halblineare Einschaltung in Pfeilfeldern
11
X2 — Xr -p(X4 — X3), X3 — Xt 2 (X4 — X2) =
I Y2 - Yt + (Y4 - Y3) , Y3 - Yt + 2 (Yt - Y2) I ’
welche für die Umhüllungsparabel in der Verzerrungsfigur gilt.
Wird sie mit der Geradengleichung behufs Ausmerzung von
verbunden, so wird X und Y durch eine gebrochene quadratische
Abhängigkeit von X mit gemeinsamem Nenner dargestellt, was
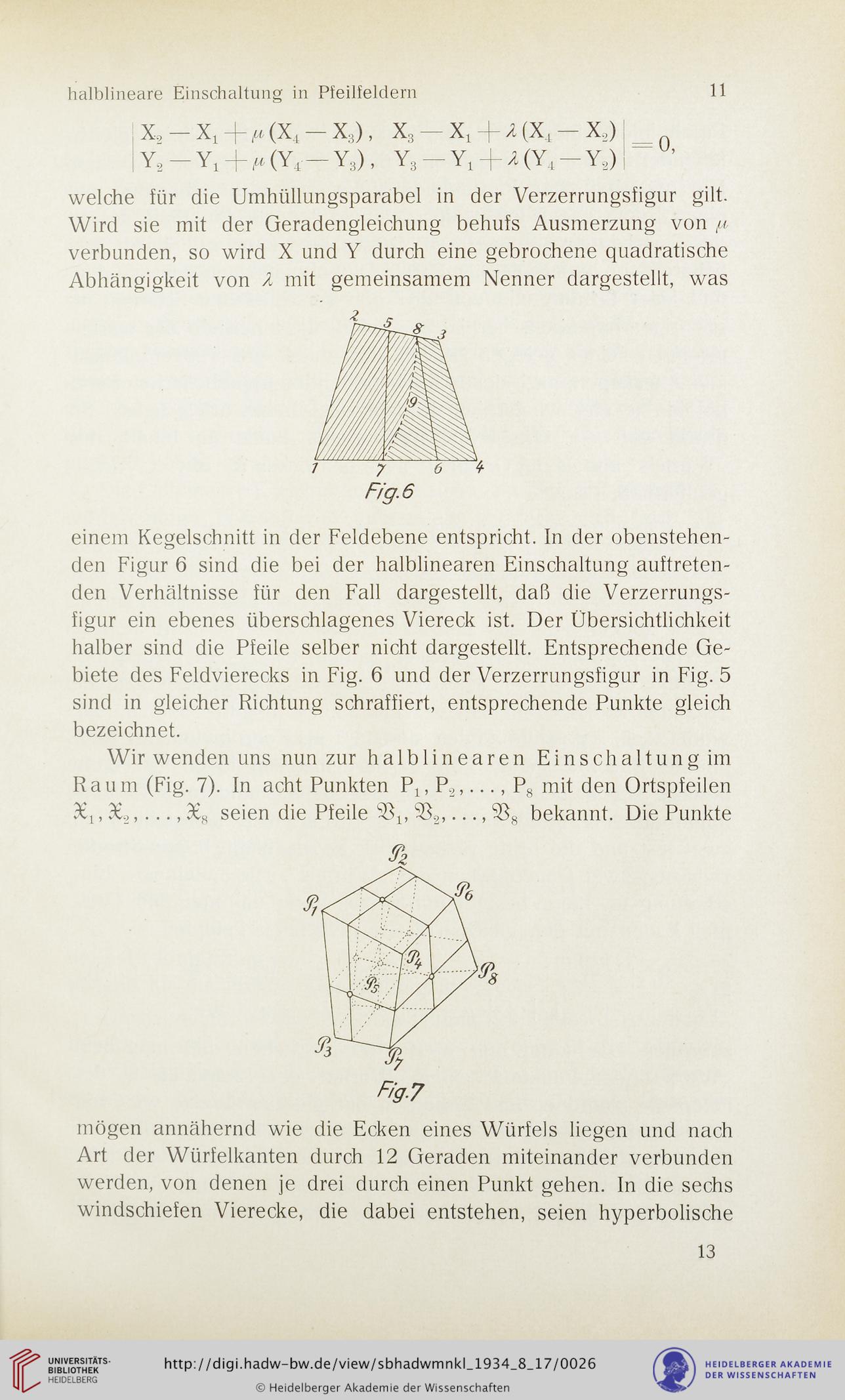
einem Kegelschnitt in der Feldebene entspricht. In der obenstehen-
den Figur 6 sind die bei der halblinearen Einschaltung auftreten-
den Verhältnisse für den Fall dargestellt, daß die Verzerrungs-
figur ein ebenes überschlagenes Viereck ist. Der Übersichtlichkeit
halber sind die Pfeile selber nicht dargestellt. Entsprechende Ge-
biete des Feldvierecks in Fig. 6 und der Verzerrungsfigur in Fig. 5
sind in gleicher Richtung schraffiert, entsprechende Punkte gleich
bezeichnet.
Wir wenden uns nun zur halb linearen Einschaltung im
Raum (Fig. 7). In acht Punkten Pn P2,..., P8 mit den Ortspfeilen
äq X8 seien die Pfeile 5S2,..., 5% bekannt. Die Punkte
mögen annähernd wie die Ecken eines Würfels liegen und nach
Art der Würfelkanten durch 12 Geraden miteinander verbunden
werden, von denen je drei durch einen Punkt gehen. In die sechs
windschiefen Vierecke, die dabei entstehen, seien hyperbolische
13
11
X2 — Xr -p(X4 — X3), X3 — Xt 2 (X4 — X2) =
I Y2 - Yt + (Y4 - Y3) , Y3 - Yt + 2 (Yt - Y2) I ’
welche für die Umhüllungsparabel in der Verzerrungsfigur gilt.
Wird sie mit der Geradengleichung behufs Ausmerzung von
verbunden, so wird X und Y durch eine gebrochene quadratische
Abhängigkeit von X mit gemeinsamem Nenner dargestellt, was
einem Kegelschnitt in der Feldebene entspricht. In der obenstehen-
den Figur 6 sind die bei der halblinearen Einschaltung auftreten-
den Verhältnisse für den Fall dargestellt, daß die Verzerrungs-
figur ein ebenes überschlagenes Viereck ist. Der Übersichtlichkeit
halber sind die Pfeile selber nicht dargestellt. Entsprechende Ge-
biete des Feldvierecks in Fig. 6 und der Verzerrungsfigur in Fig. 5
sind in gleicher Richtung schraffiert, entsprechende Punkte gleich
bezeichnet.
Wir wenden uns nun zur halb linearen Einschaltung im
Raum (Fig. 7). In acht Punkten Pn P2,..., P8 mit den Ortspfeilen
äq X8 seien die Pfeile 5S2,..., 5% bekannt. Die Punkte
mögen annähernd wie die Ecken eines Würfels liegen und nach
Art der Würfelkanten durch 12 Geraden miteinander verbunden
werden, von denen je drei durch einen Punkt gehen. In die sechs
windschiefen Vierecke, die dabei entstehen, seien hyperbolische
13