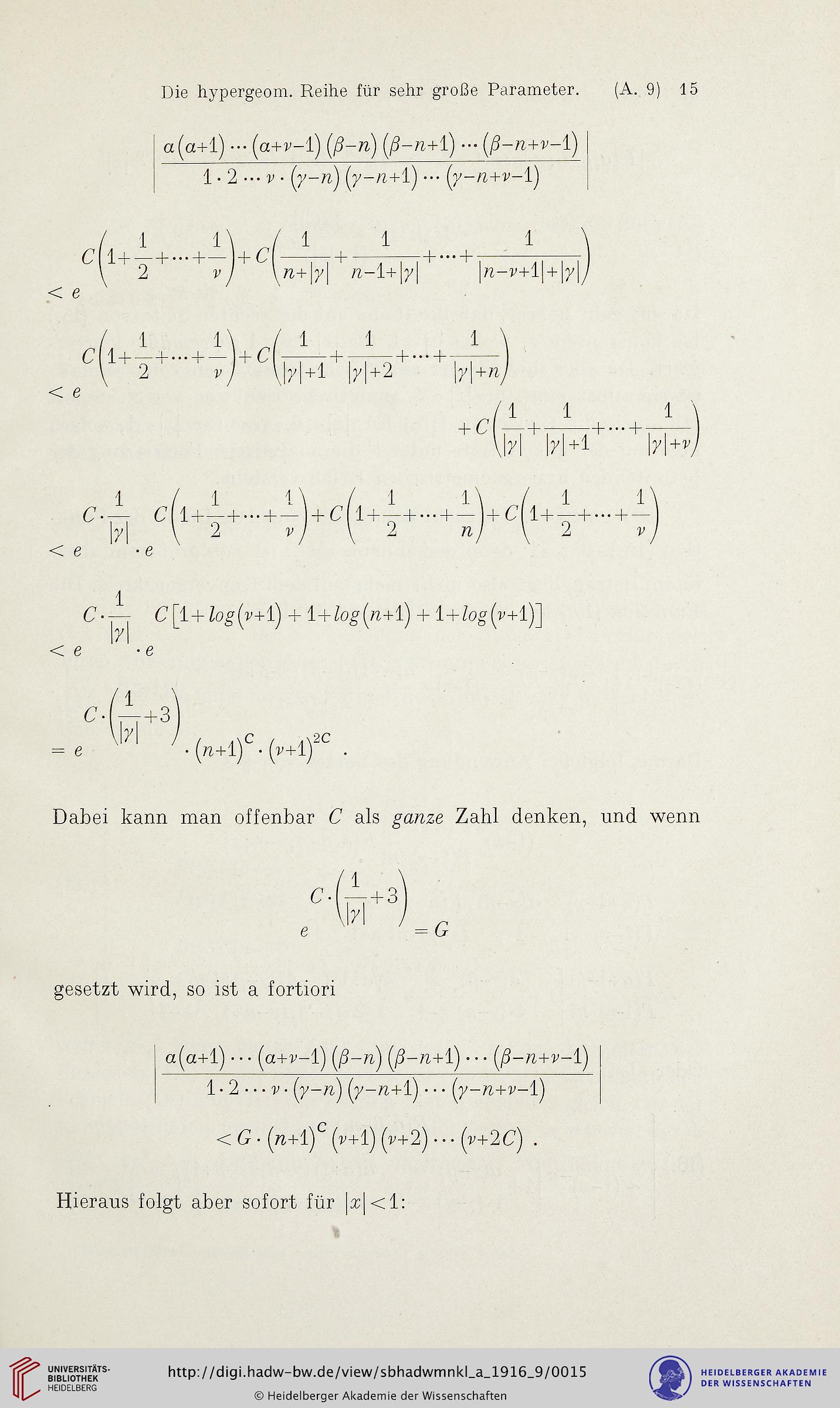DOI Page / Citation link:
https://doi.org/10.11588/diglit.34894#0015
Die hypergeom. Reihe für sehr große Parameter. (A. 9) 15
:(a+l) --- (a+r-l) (^-/z+l) --- (/5-^+r-l)
1 - 2 --- r - (y-^) (/-/i+l) --- (y-^+r-l)
< e
, i 1\ / 1 1 1
ü[l + —-!—)+P[ —,—^-,—j—r + "*Ai <1 ;
2 r / \^+]yl ^-1+]/] ]^-r+lj + )
dl + 4+... + -^+cf—L+; ^
< e
\ 2 r/ \]/)+l l/j+2 ]/)+n
, 1 1
+ c +
/[ ]/]+! l/j+r
< e - e
1
C-j-j C [1+ + l+fo^^+l) + l+fog(r+l)]
< e - e
(n+i)^ - (r+1) ^ -
Dabei kann man offenbar C als g%H.ze Zahl denken, und wenn
gesetzt wird, so ist a fortiori
t(a+l) - - - (a+r-1) (^-n) (^-n+l) - - - (^-72+r-l)
1 - 2 - - - r - (/-n.) (y-7?.+l) - - - f/-7Z+r-l)
< C - (^+1)^ (r+1) (r+2) - - - (r+2C) .
Hieraus folgt aber sofort für
:(a+l) --- (a+r-l) (^-/z+l) --- (/5-^+r-l)
1 - 2 --- r - (y-^) (/-/i+l) --- (y-^+r-l)
< e
, i 1\ / 1 1 1
ü[l + —-!—)+P[ —,—^-,—j—r + "*Ai <1 ;
2 r / \^+]yl ^-1+]/] ]^-r+lj + )
dl + 4+... + -^+cf—L+; ^
< e
\ 2 r/ \]/)+l l/j+2 ]/)+n
, 1 1
+ c +
/[ ]/]+! l/j+r
< e - e
1
C-j-j C [1+ + l+fo^^+l) + l+fog(r+l)]
< e - e
(n+i)^ - (r+1) ^ -
Dabei kann man offenbar C als g%H.ze Zahl denken, und wenn
gesetzt wird, so ist a fortiori
t(a+l) - - - (a+r-1) (^-n) (^-n+l) - - - (^-72+r-l)
1 - 2 - - - r - (/-n.) (y-7?.+l) - - - f/-7Z+r-l)
< C - (^+1)^ (r+1) (r+2) - - - (r+2C) .
Hieraus folgt aber sofort für