22 (A. 9)
WlRTZ und HÜGELER:
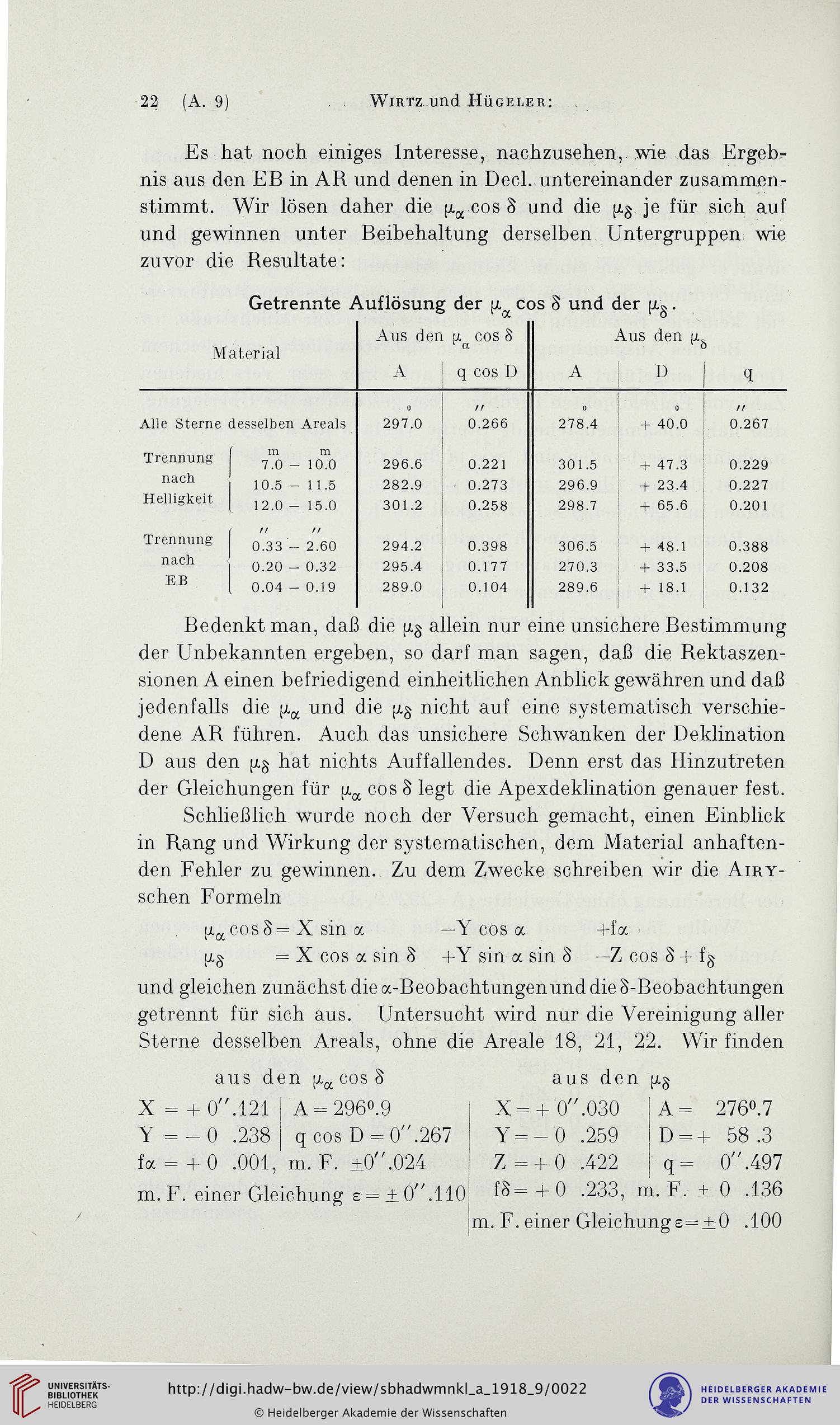
Es hat noch einiges Interesse, nachzusehen, wie das Ergeb-
nis aus den EB in AR und denen in Deel, untereinander zusammen-
stimmt. Wir lösen daher die ^ cos § und die [j.§ je für sich auf
und gewinnen unter Beibehaltung derselben Untergruppen wie
zuvor die Resultate:
Getrennte Auflösung
Material
Aus d
A
Alle Sterne desselben
Areals
297.0
Trennung
7.0 -
10U
296.6
nach
10.5 -
1 1.5
282.9
Helligkeit
12.0 -
15.0
301.2
Trennung
0.33 -
2.60
294.2
nach
0.20 -
0.32
295.4
EB
0.04 -
0.19
289.0
der cos § und der ^.
^ COS §
Aus den [j.^
COS D
A
D
q
„
„
o
„
0.266
278.4
+ 40.0
0.267
0.221
301.5
+ 47.3
0.229
0.273
296.9
+ 23.4
0.227
0.258
298.7
+ 65.6
0.201
0.398
306.5
+ 48.1
0.388
0.177
270.3
+ 33.5
0.208
0.104
289.6
+ 18.1
0.132
Bedenkt man, daß die allein nur eine unsichere Bestimmung
der Unbekannten ergeben, so darf man sagen, daß die Rektaszen-
sionen A einen befriedigend einheitlichen Anblick gewähren und daß
jedenfalls die und die nicht auf eine systematisch verschie-
dene AR führen. Auch das unsichere Schwanken der Deklination
D aus den hat nichts Auffallendes. Denn erst das Hinzutreten
der Gleichungen für ^ cos § legt die Apexdeklination genauer fest.
Schließlich wurde noch der Versuch gemacht, einen Einblick
in Rang und Wirkung der systematischen, dem Material anhaften-
den Fehler zu gewinnen. Zu dem Zwecke schreiben wir die AiRY-
schen Formeln
q^cos8=Xsina —Ycosa +fa
= X cos a sin § +Y sin a sin § —Z cos 8 + f§
und gleichen zunächst die a-Beobachtungenund die 8-Beobachtungen
getrennt für sich aus. Untersucht wird nur die Vereinigung aller
Sterne desselben Areals, ohne die Areale 18, 21, 22. Wir finden
aus den cos 8
X - + 0".121 } A = 296t9
Y= — 0 .238 qcosD = 0".267
fa = + 0 .001, m. F. +0".024
m. F. einer Gleichung s = + 0".110
aus den
X = +0".030 A = 2760.7
Y = - 0 .259 ^ D = + 58 .3
Z = + 0 .422 ! q= 0".497
f8 = +0 .233, m. F. + 0 .136
in. F. einer Gleichung s—±0 .100
WlRTZ und HÜGELER:
Es hat noch einiges Interesse, nachzusehen, wie das Ergeb-
nis aus den EB in AR und denen in Deel, untereinander zusammen-
stimmt. Wir lösen daher die ^ cos § und die [j.§ je für sich auf
und gewinnen unter Beibehaltung derselben Untergruppen wie
zuvor die Resultate:
Getrennte Auflösung
Material
Aus d
A
Alle Sterne desselben
Areals
297.0
Trennung
7.0 -
10U
296.6
nach
10.5 -
1 1.5
282.9
Helligkeit
12.0 -
15.0
301.2
Trennung
0.33 -
2.60
294.2
nach
0.20 -
0.32
295.4
EB
0.04 -
0.19
289.0
der cos § und der ^.
^ COS §
Aus den [j.^
COS D
A
D
q
„
„
o
„
0.266
278.4
+ 40.0
0.267
0.221
301.5
+ 47.3
0.229
0.273
296.9
+ 23.4
0.227
0.258
298.7
+ 65.6
0.201
0.398
306.5
+ 48.1
0.388
0.177
270.3
+ 33.5
0.208
0.104
289.6
+ 18.1
0.132
Bedenkt man, daß die allein nur eine unsichere Bestimmung
der Unbekannten ergeben, so darf man sagen, daß die Rektaszen-
sionen A einen befriedigend einheitlichen Anblick gewähren und daß
jedenfalls die und die nicht auf eine systematisch verschie-
dene AR führen. Auch das unsichere Schwanken der Deklination
D aus den hat nichts Auffallendes. Denn erst das Hinzutreten
der Gleichungen für ^ cos § legt die Apexdeklination genauer fest.
Schließlich wurde noch der Versuch gemacht, einen Einblick
in Rang und Wirkung der systematischen, dem Material anhaften-
den Fehler zu gewinnen. Zu dem Zwecke schreiben wir die AiRY-
schen Formeln
q^cos8=Xsina —Ycosa +fa
= X cos a sin § +Y sin a sin § —Z cos 8 + f§
und gleichen zunächst die a-Beobachtungenund die 8-Beobachtungen
getrennt für sich aus. Untersucht wird nur die Vereinigung aller
Sterne desselben Areals, ohne die Areale 18, 21, 22. Wir finden
aus den cos 8
X - + 0".121 } A = 296t9
Y= — 0 .238 qcosD = 0".267
fa = + 0 .001, m. F. +0".024
m. F. einer Gleichung s = + 0".110
aus den
X = +0".030 A = 2760.7
Y = - 0 .259 ^ D = + 58 .3
Z = + 0 .422 ! q= 0".497
f8 = +0 .233, m. F. + 0 .136
in. F. einer Gleichung s—±0 .100