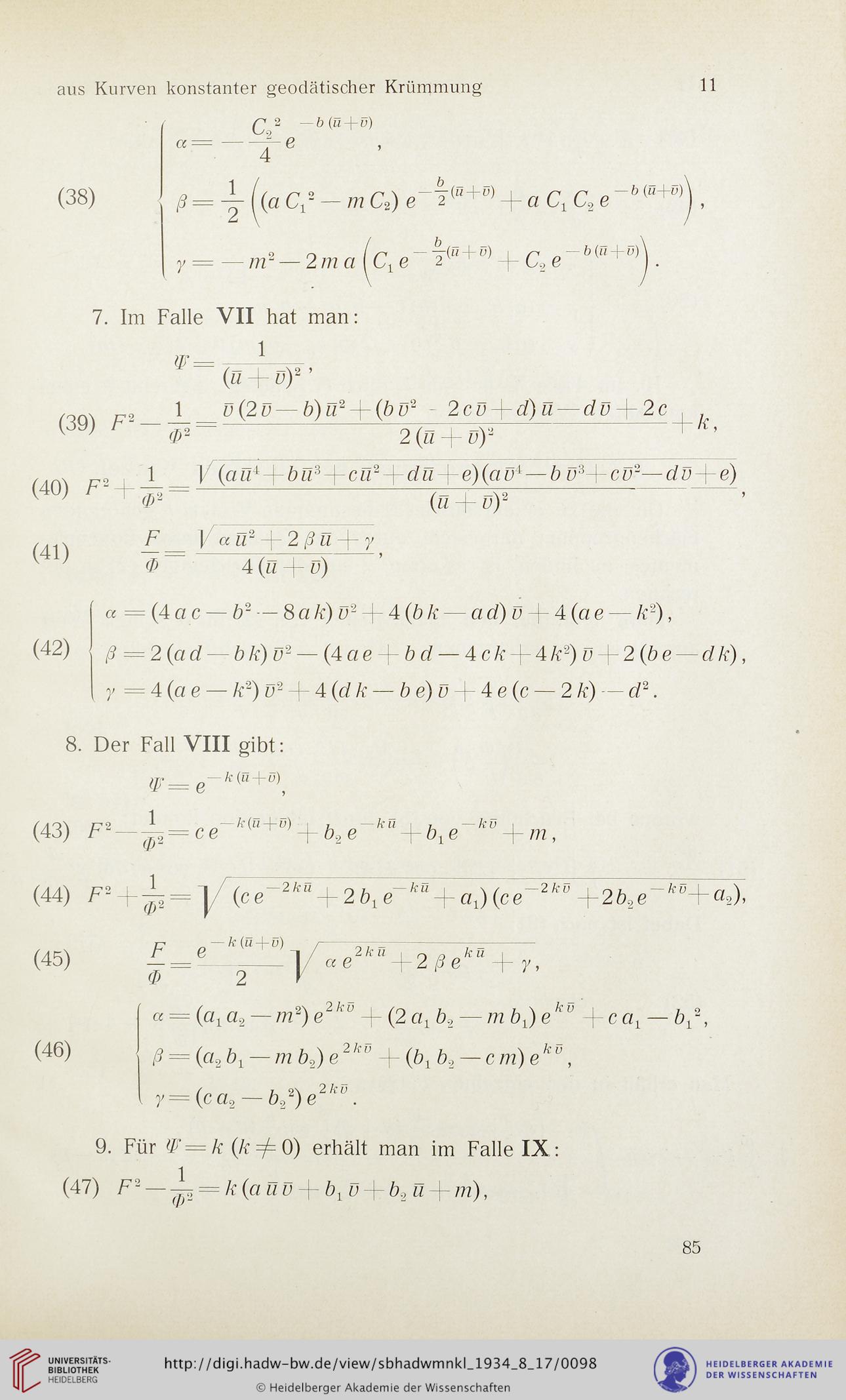aus Kurven konstanter geodätischer Krümmung
11
(38)
Q2 — b(u + v)
a =-f- e
4
ß = -j- fra C,- - m Cä) e-|(”+tl) + a C, C, e ,
y = — m•- — 2 m a F e ~ l<0+a> + C., e ~b ("+'4 .
7. Im Falle VII hat man:
(ü + ü)a ’
1 v(2v—b)ii2-\-(bü2 - 2cv-\-d)ü— dü-\-2c
02 2 (ü 4~ ü)2
y =4 (cte — k2) n2 + 4 (rf /< — b e) v + 4 e (c — 2 k) — d2.
(40) f*+±-
]/ (aid bii3 4 cu24du4e)(an4 — b n34 cu2— du-\-e)
(ü 4 n)2
(41)
F
(J)~
]/ cc ll2 ß- 2 ß ll-\- y
4 (ii 4~ ü)
a = (4
cic — b2 — 8 a k) v2 4- 4 (b k — ad)v 4
- 4 (ci e — k2),
(42)
ß = 2(cid —bk) u2 — (4ae-\-bd — 4 c k + 4 k2) v 4- 2 (b e — d k),
8. Der Fall VIII gibt:
— k (u+d)
(43) F* - dj = c bi e+ b[ e-k» + m,
(44)
F
4=]A
/fö+a2),
(45)
(46)
F e^'V 2kiF F~F~ku
_= ___ _ y ae +2/?e +y,
a = (a1 a2 — m2) e2kv (2 ar b., — m b^ehv 4c ai — 42 >
ß = (a2 bv — m bß) e2kv -\-(b1b2 — c m) eku,
y=(ca2 — b,2) e21'".
9. Für F=k (k=/=Q) erhält man im Falle IX:
(47) F2-l = /{(a ^4 5 + b2 ii + m),
85
11
(38)
Q2 — b(u + v)
a =-f- e
4
ß = -j- fra C,- - m Cä) e-|(”+tl) + a C, C, e ,
y = — m•- — 2 m a F e ~ l<0+a> + C., e ~b ("+'4 .
7. Im Falle VII hat man:
(ü + ü)a ’
1 v(2v—b)ii2-\-(bü2 - 2cv-\-d)ü— dü-\-2c
02 2 (ü 4~ ü)2
y =4 (cte — k2) n2 + 4 (rf /< — b e) v + 4 e (c — 2 k) — d2.
(40) f*+±-
]/ (aid bii3 4 cu24du4e)(an4 — b n34 cu2— du-\-e)
(ü 4 n)2
(41)
F
(J)~
]/ cc ll2 ß- 2 ß ll-\- y
4 (ii 4~ ü)
a = (4
cic — b2 — 8 a k) v2 4- 4 (b k — ad)v 4
- 4 (ci e — k2),
(42)
ß = 2(cid —bk) u2 — (4ae-\-bd — 4 c k + 4 k2) v 4- 2 (b e — d k),
8. Der Fall VIII gibt:
— k (u+d)
(43) F* - dj = c bi e+ b[ e-k» + m,
(44)
F
4=]A
/fö+a2),
(45)
(46)
F e^'V 2kiF F~F~ku
_= ___ _ y ae +2/?e +y,
a = (a1 a2 — m2) e2kv (2 ar b., — m b^ehv 4c ai — 42 >
ß = (a2 bv — m bß) e2kv -\-(b1b2 — c m) eku,
y=(ca2 — b,2) e21'".
9. Für F=k (k=/=Q) erhält man im Falle IX:
(47) F2-l = /{(a ^4 5 + b2 ii + m),
85